ВАРІАНТ № 4
1. Обчислити визначники
; 
.
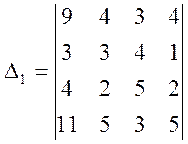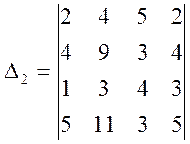2. Розв’язати системи лінійних алгебраїчних рівнянь
а) методом Крамера;
б) матричним методом;
в) методом Гауса.
1) 
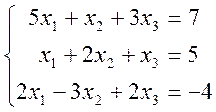; 2) 
.
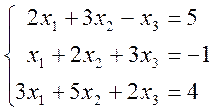3. Напишіть розклад вектору 
за векторами 
, якщо 
, 
, 
, 
.
4. В базисі 
оператор 
має
матрицю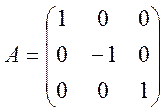 
. Знайти матрицю 
оператору
в базисі 
, 
, 
.
5. Привести квадратичну форму 
до канонічного виду, приводячи
матрицю квадратичної форми 
до діагонального виду й
вибираючи в якості базисних векторів власні вектори матриці .
6. Пряма 
перетинає осі 
й 
в точках
й 
. Точка 
поділяє 
у відношенні
. Написати рівняння перпендикуляра, поновленого
в точці до прямої .
7. Побудувати лінії, які визначаються рівняннями:
|
а) |
б) |
в) |
8. Знайти вказані границі (не користуючись правилом Лопиталю).
|
а) |
б) |
в) |
|
г) |
д) |
е) |
9. Задана функція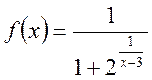 
. Дослідити її на
неперервність й встановити характер точок розриву. Зробити схематичне
креслення.
10. Знайти похідні 
заданих функцій. В
завданнях а), г) знайти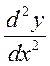 
.
|
а) |
б) |
в) |
|
г) |
д) |
е) |
11. Знайти найбільше й найменше значення функції 
на
відрізку
.
12. Провести повне дослідження й побудувати графік функції 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
;
;
.
;
;
;
;
;
.
;
;
;
;
;
.