






Практичне заняття №2.
“Приватні похідні і диференціал функції. Приватні похідні вищих порядків. Диференціювання складних функцій ”
Приватні похідні і диференціал функції
Приватною
похідною від
функції ![]() по незалежної перемінної х
називається похідна
по незалежної перемінної х
називається похідна
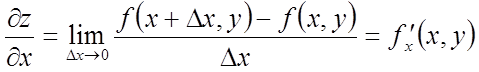
обчислена при постійному у.
Приватною похідною по у називається похідна
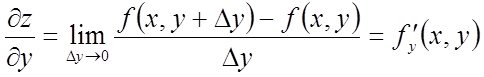
обчислена при постійному х.
Для приватних похідних справедливі звичайні правила і формули диференціювання.
Приклад 1.
![]() . Знайти
. Знайти ![]() і
і ![]() .
.
Рішення. Розглядаючи у як
постійну величину, одержимо 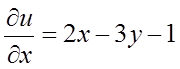 . Розглядаючи х
як постійну, знайдемо
. Розглядаючи х
як постійну, знайдемо 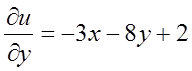 .
.
Приклад 2.
![]() . Знайти
. Знайти ![]() і
і ![]() .
.
Рішення. Маємо
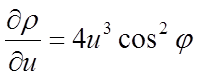 ,
, 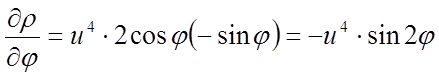
Приклад 3.
Показати,
що функція ![]() задовольняє рівнянню
задовольняє рівнянню 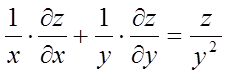 .
.
Рішення. Знаходимо
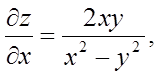
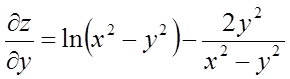 .
.
Підставимо знайдені вираження в знайдену частину рівняння:
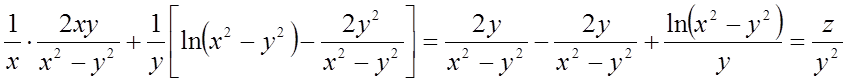
Повний диференціал.
Повним
збільшенням
функція ![]() в крапці
в крапці ![]() називається
різниця
називається
різниця ![]() , де
, де ![]() і
і ![]() – довільні збільшення аргументів.
– довільні збільшення аргументів.
Функція ![]() називається диференціюємою у крапці
називається диференціюємою у крапці
![]() , якщо в цій крапці повне збільшення
можна представити у виді
, якщо в цій крапці повне збільшення
можна представити у виді
![]() ,
,
де ![]() .
.
Повним
диференціалом
функції ![]() називається головна частина повного
збільшення
називається головна частина повного
збільшення ![]() , лінійна щодо збільшень аргументів
, лінійна щодо збільшень аргументів ![]() і
і ![]() , тобто
, тобто ![]() .
.
Диференціали
незалежних перемінних збігаються з їх збільшеннями, тобто ![]() і
і ![]() .
.
Повний
диференціал функції ![]() обчислюється по формулі
обчислюється по формулі
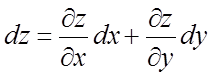 .
.
Аналогічно, повний
диференціал функції трьох аргументів ![]() обчислюється по
формулі
обчислюється по
формулі
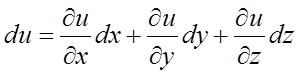 .
.
При досить малому
![]() для диференціюємої функції
для диференціюємої функції ![]() справедливі наближені рівності
справедливі наближені рівності
![]()
![]() .
.
Приклад 4.
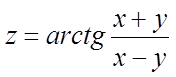 . Знайти
. Знайти ![]() .
.
Рішення. Знайдемо приватні похідні:
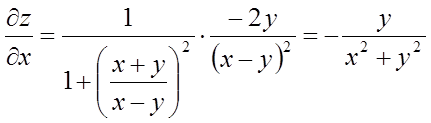 ,
,
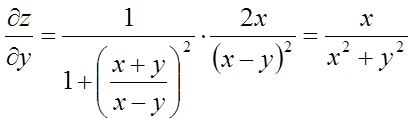 .
.
Отже,
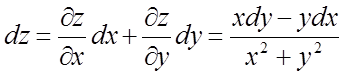 .
.
Приклад 5.
![]() . Знайти
. Знайти ![]() .
.
Рішення. Маємо 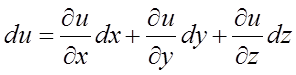 , де
, де
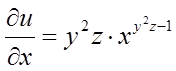 ,
, 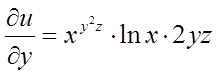 ,
, 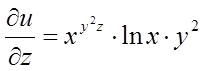 .
.
Отже,
![]() .
.
Приклад 6.
Обчислити приблизно ![]() , виходячи зі значення функції
, виходячи зі значення функції ![]() при х=1, у=1.
при х=1, у=1.
Рішення. Значення функції ![]() при х=1, у=1 є
при х=1, у=1 є ![]() . Знайдемо збільшення функції
. Знайдемо збільшення функції ![]() при
при ![]() ,
, ![]() :
:
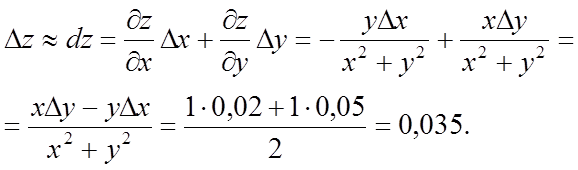
Отже, ![]() .
.
Приватні похідні і диференціали вищих порядків.
Приватними
похідними другого порядку від функції ![]() називаються приватні
похідні від її приватних похідних першого порядку.
називаються приватні
похідні від її приватних похідних першого порядку.
Позначення приватних похідних другого порядку:
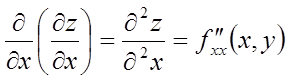 ;
;
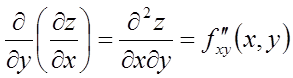 ;
;
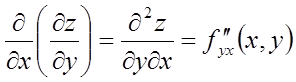 ;
;
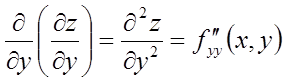 .
.
Аналогічно визначаються і позначаються приватні похідні третього і вищого порядків, наприклад;
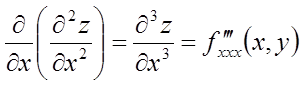 ;
;
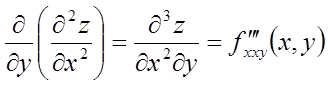 і т.д.
і т.д.
так називані «змішані» похідні, що
відрізняються друг від друга лише послідовністю диференціювання, рівні між
собою, якщо вони безперервні, наприклад, 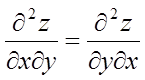 .
.
Диференціалом
другого порядку від функції ![]() називається диференціал від її
повного диференціала, тобто
називається диференціал від її
повного диференціала, тобто ![]() .
.
Аналогічно
визначаються диференціали третього і вищого порядків: ![]() ;
узагалі,
;
узагалі, ![]() .
.
Якщо х и у
– незалежні перемінні і функція ![]() має
безперервні приватні похідні, то диференціали вищих порядків обчислюються по
формулах:
має
безперервні приватні похідні, то диференціали вищих порядків обчислюються по
формулах:
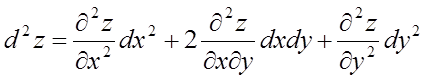 ;
;
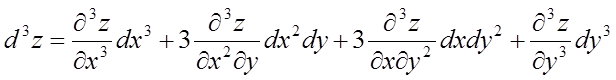 ;
;
узагалі, має місце символічна формула
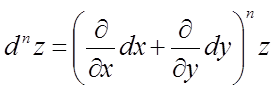 ,
,
яка формально розкривається по біноміальному законі.
Приклад 7.
![]() . Знайти
. Знайти 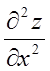 ,
, 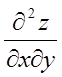 ,
, 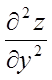 .
.
Рішення. Знайдемо приватні похідні:
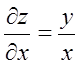 ;
; 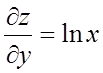 .
.
Диференціюючи повторно, одержимо
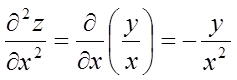 ;
;
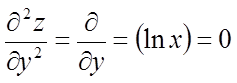 ;
;
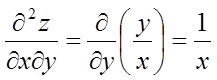 .
.
Приклад 8.
![]() . Знайти
. Знайти ![]() .
.
Рішення. Маємо
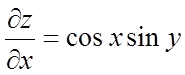 ;
; 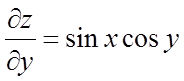 ,
,
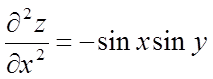 ,
, 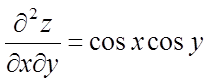 ,
, 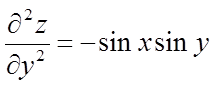 ,
,
![]() .
.
Приклад 9.
![]() . Знайти
. Знайти ![]() .
.
Рішення. Маємо
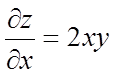 ,
, 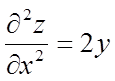 ,
, 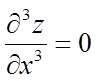 .
.
Диференціювання складних функцій.
Нехай ![]() , де
, де ![]() ,
, ![]() і функції
і функції ![]() ,
, ![]() ,
, ![]() дифференціюємі.
дифференціюємі.
Тоді похідна
складної функції ![]() обчислюється по формулі
обчислюється по формулі
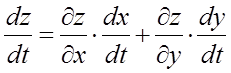 .
.
Якщо ![]() , де
, де ![]() , то повна похідна від z по х
знаходиться по формулі
, то повна похідна від z по х
знаходиться по формулі
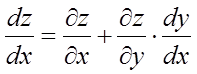 .
.
Якщо ж ![]() , де
, де ![]() ,
, ![]() , то приватні похідні виражаються так:
, то приватні похідні виражаються так:
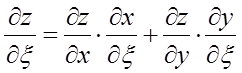 ,
,
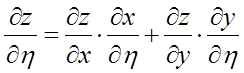 .
.
Приклад 10.
![]() , де
, де ![]() ,
, ![]() . Знайти
. Знайти ![]() .
.
Рішення. Маємо
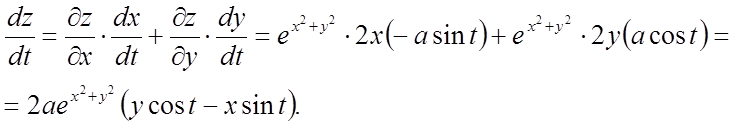
Виразивши х и у через t, одержимо
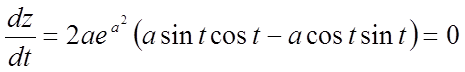 .
.
Приклад 11.
![]() , де
, де
![]() . Знайти
. Знайти ![]() ,
, ![]() .
.
Рішення. Маємо 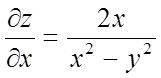 . Використовуючи формулу повної похідної,
знаходимо
. Використовуючи формулу повної похідної,
знаходимо
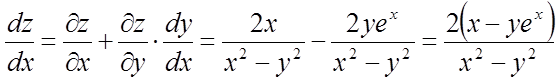
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.