






Практическая работа №3
Пример 1. Вероятность сохранения килограмма картошки до весны равна 0,4. Какова вероятность того, что будет сохранено 293000 килограмма картошки, если всего собрали 400000 килограмма?
Решение.
По условию n=400000, p=0,4,
q=1-p=0,6, m=239000. Необходимо найти ![]() .
Воспользуемся локальной предельной теоремой Муавра-Лапласа:
.
Воспользуемся локальной предельной теоремой Муавра-Лапласа: 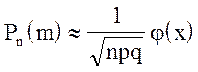 , где
, где 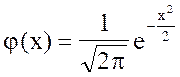 ,
причем значение аргумента находят по формуле:
,
причем значение аргумента находят по формуле: 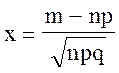 .
.
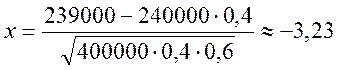 .
.
По таблицам плотности нормального закона интеграла вероятности
![]() .
.
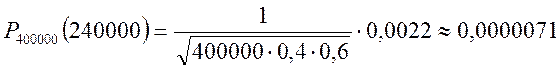 .
.
Ответ:
![]() .
.
Пример 2. Вероятность всхожести семени пиона в теплице равна 0,8. Найти вероятность того, что из 2000 посаженных семян взойдет не менее 1550.
Решение.
По условию ![]() . Необходимо
найти
. Необходимо
найти ![]() . Воспользуемся интегральной теоремой
Лапласа.
. Воспользуемся интегральной теоремой
Лапласа.
![]() ,
,
где
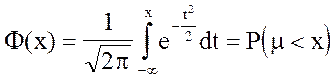 - функция Лапласа,
- функция Лапласа,
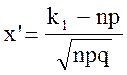 ,
, 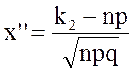 .
.
Найдем
![]() :
:
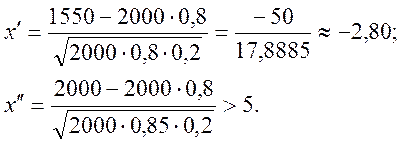
Так
как ![]() , то возмем
, то возмем
![]()
![]() .
.
По таблицам плотности нормального закона интеграла вероятности найдем ![]() . Искомая вероятность
. Искомая вероятность ![]()
Ответ:
![]()
Пример 3. Со склада в магазин отправлено 1000 ящиков фарфора. Вероятность повреждения содержимого ящика в пути равна 0,998. Найти вероятность того, что целыми прибудут хотя бы 5 ящиков.
Решение.
По условию n=1000. События «поврежденное
содержимое ящика» и «целое содержимое ящика» противоположны, и так как
необходимо найти вероятность того, что целыми прибудут хотя бы 5 ящиков, то
следует принять p=1-0,998=0,002. Так как вероятность мала, а число n
велико, то воспользуемся теоремой Пуассона: если при n независимых
испытаниях некоторое событие происходит с вероятностью p близкой к
нулю, то при достаточно большом n вероятность осуществления события m раз
приближенно равна: 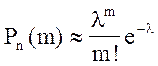 , где
, где ![]() . Найдем
l:
. Найдем
l: ![]() .
Необходимо найти вероятность появления события хотя бы в 5 испытаниях, т.е.
.
Необходимо найти вероятность появления события хотя бы в 5 испытаниях, т.е.
![]() .
.
Для удобства вычислений и исходя из смысла вероятности обратного события можно сделать переход
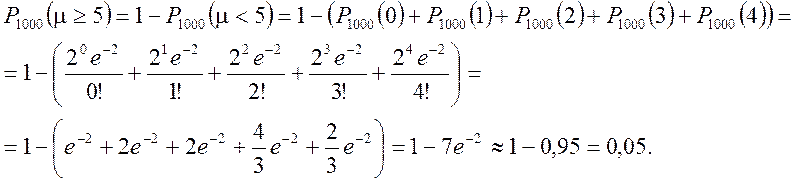 Ответ:
Ответ: ![]() .
.
Пример 4. 200 солдат стреляют по команде из орудий. Вероятность выстрела не точно по команде каждого солдата 0,25. Найти вероятность того, что относительная частота несвоевременного выстрела отклонится от его вероятности не более чем на 0,1225, если учесть, что все солдаты стреляют одинаково.
Решение.
По условию: n=200; p=0,25; q=0,75; e=0,1225. Найдем вероятность P отклонения частоты от вероятности. Воспользуемся формулой вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях:
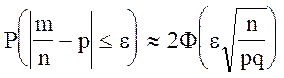 .
.
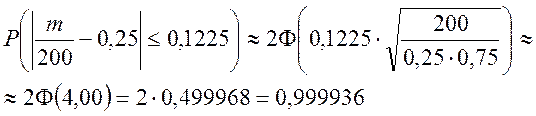 .
.
Ответ:
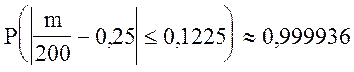 .
.
Пример 5. Прыгает
196 парашютистов. Вероятность точного приземления на отведенный участок равна
0,98. Найти такое положительное число ![]() , чтобы
с вероятностью 0,1586 абсолютная величина отклонения относительной частоты
появления точного приземления парашютиста от вероятности его появления 0,98 не
превысила
, чтобы
с вероятностью 0,1586 абсолютная величина отклонения относительной частоты
появления точного приземления парашютиста от вероятности его появления 0,98 не
превысила ![]() .
.
Решение.
По условию: n=196; p=0,98; q=0,02; P=0,1586. Найти e. Воспользуемся формулой вероятности отклонения относительной частоты от постоянной вероятности в независимых испытаниях:
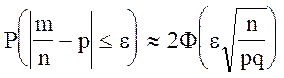 .
.
Исходя из условия
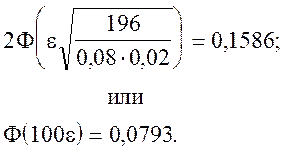
По таблицам плотности нормального закона интеграла вероятности: ![]() ; Следовательно 100e=0,20; e =0,002.
; Следовательно 100e=0,20; e =0,002.
Ответ:
![]() .
.
Пример 6. При увеличении напряжения в два раза может произойти разрыв электрической цепи вследствие выхода из строя одного из трех последовательно соединенных элементов соответственно с вероятностями 0,3; 0,4; 0,5. Определить вероятность того, что не будет разрыв цепи.
Решение.
Пусть события ![]() ,
, ![]() ,
, ![]() означают
выход из строя соответственно первого, второго и третьего элементов. Их
вероятности по условию равны:
означают
выход из строя соответственно первого, второго и третьего элементов. Их
вероятности по условию равны: ![]() ,
, ![]() ,
, ![]() . Тогда
вероятность события
. Тогда
вероятность события ![]() , противоположного событию
, противоположного событию ![]() (первый элемент не вышел из строя), будет
равна
(первый элемент не вышел из строя), будет
равна ![]() , аналогично вычисляются
, аналогично вычисляются ![]() ,
, ![]() .
Искомая вероятность равна вероятности того, что не выйдут из строя все три
элемента. Так как события
.
Искомая вероятность равна вероятности того, что не выйдут из строя все три
элемента. Так как события ![]() ,
, ![]() ,
, ![]() независимы,
то по теореме умножения независимых событий имеем
независимы,
то по теореме умножения независимых событий имеем
![]() .
.
Ответ:
![]() .
.
Пример 7. В партии из 50 деталей 5 нестандартных. Определить вероятность того, что среди выбранных на удачу для проверки шести деталей две окажутся нестандартными.
Решение.
Элементарным исходом является выборка любых шести
изделий из пятидесяти. Число ![]() всех таких исходов,
очевидно, равно числу сочетаний из пятидесяти по шесть, т.е. С
всех таких исходов,
очевидно, равно числу сочетаний из пятидесяти по шесть, т.е. С![]() . Нас интересует событие
. Нас интересует событие ![]() , состоящее в том, что две из шести деталей
нестандартные. Благоприятным исходом для события
, состоящее в том, что две из шести деталей
нестандартные. Благоприятным исходом для события ![]() является
любые шесть деталей, из которых две нестандартные и четыре - стандартные. Такого рода групп по шесть деталей имеется
является
любые шесть деталей, из которых две нестандартные и четыре - стандартные. Такого рода групп по шесть деталей имеется ![]() (так как
(так как ![]() - число всевозможных пар нестандартных деталей, а
- число всевозможных пар нестандартных деталей, а ![]() - число всевозможных
четверок стандартных деталей и каждая пара нестандартных деталей может
оказаться в одной группе с каждой четверкой стандартных деталей). Таким
образом,
- число всевозможных
четверок стандартных деталей и каждая пара нестандартных деталей может
оказаться в одной группе с каждой четверкой стандартных деталей). Таким
образом, 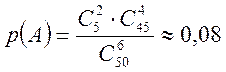 .
.
Пример 8. Вероятность того, что в некоторой местности каждый из 30000 жителей окажется больным туберкулезом, равна 0,00015. Найти границу отклонения частоты появления заболевания от его вероятности по абсолютной величине, если это отклонение можно ожидать с вероятностью, не меньшей 0,98.
Решение.
Для
нахождения e воспользуемся вторым неравенством Чебышева: если DX<¥, то![]() .
Подставляя в него данные задачи (по условию
.
Подставляя в него данные задачи (по условию ![]() ,
, ![]() ,
, ![]() ).
).
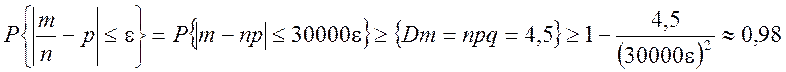
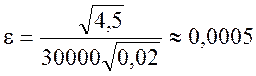 .
.
Ответ:
![]() .
.
Пример 9. Вероятность
того, что при проникновении в помещение постороннего сработает сигнализация,
равна 0,986. Для срабатывания сигнализации установлено два независимо
работающих сигнализатора. Вероятность срабатывания одного из них – 0,9. Про
другой известно, что любое число успешных его испытаний, распределенных по
нормальному закону, отличается по модулю от среднего менее чем на 3. Определить
для этого сигнализатора ![]() .
.
Решение.
По условию задачи сигнализаторы работают независимо,
следовательно, срабатывание одного из них не исключает срабатывание другого. По
формуле сложения вероятностей совместных событий имеем: ![]()
![]() . Далее используя формулу
. Далее используя формулу ![]() получаем:
получаем: ![]() .
.
Ответ:
![]() .
.
Пример 10. Учитель проверяет диктант. При этом вероятность заметить ошибку равна 0,95. Найти вероятность того, что из 8 допущенных ошибок преподаватель заметит не более половины?
Решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.