По условию ![]() ;
; ![]() ;
; ![]() .
Половина от восьми будет четыре, следовательно,
.
Половина от восьми будет четыре, следовательно, ![]() .
Необходимо найти
.
Необходимо найти ![]() . Так как вероятность заметить
ошибку постоянна и не имеет значения последовательность обнаружения или пропуск
ошибок, то можно воспользоваться формулой Бернулли. Искомая вероятность:
. Так как вероятность заметить
ошибку постоянна и не имеет значения последовательность обнаружения или пропуск
ошибок, то можно воспользоваться формулой Бернулли. Искомая вероятность:
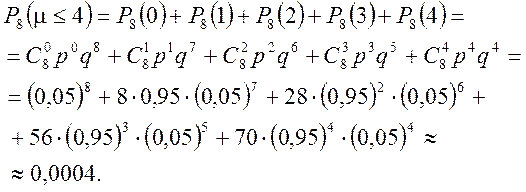
Ответ: ![]()
Пример 11. Какова вероятность того, что выбранное на удачу изделие окажется первосортным, если известно, что 3% всей продукции составляют нестандартные изделия, а 75% стандартных изделий удовлетворяют требованиям первого сорта?
Решение.
Обозначим через ![]() событие,
заключающееся в том, что выбранное изделие - стандартное, а
через
событие,
заключающееся в том, что выбранное изделие - стандартное, а
через ![]() - что изделие
первосортное. Тогда
- что изделие
первосортное. Тогда
![]() ,
, ![]() .
.
Искомая
вероятность ![]() .
.
Ответ:
![]() .
.
Пример 12. В урне 30 шаров, из них 5 красных, 10 - синих, 14 - зеленых и один - белый. Какова вероятность того, что в первый раз будет вынут красный шар (событие А), во второй раз - синий (событие В) и в третий - зеленый (событие С), если извлеченные из урны шары обратно не возвращаются.
Решение.
Вероятность того, что первоначально будет вынут
красный шар, равна 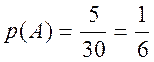 . Вероятность вытянуть синий шар
при условии, что первоначально из урны был вынут красный, равна
. Вероятность вытянуть синий шар
при условии, что первоначально из урны был вынут красный, равна 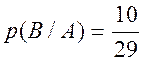 , так как после изъятия красного шара в
урне осталось 29 шаров, из них - 10 синих. Вероятность вытянуть
в первый раз красный шар, а во второй синий, равна:
, так как после изъятия красного шара в
урне осталось 29 шаров, из них - 10 синих. Вероятность вытянуть
в первый раз красный шар, а во второй синий, равна:  .
Вероятность вытянуть из урны зеленый шар, после того как были извлечены красный
и синий шары, равна
.
Вероятность вытянуть из урны зеленый шар, после того как были извлечены красный
и синий шары, равна  (после изъятия из урны красного
и синего шаров осталось 28 шаров, из них 14 - зеленых). Отсюда
вероятность вытянуть в первый раз красный, во второй - синий и третий - зеленый шары равна
(после изъятия из урны красного
и синего шаров осталось 28 шаров, из них 14 - зеленых). Отсюда
вероятность вытянуть в первый раз красный, во второй - синий и третий - зеленый шары равна
![]() .
.
Пример 13. Достаточным условием сдачи коллоквиума является ответ на один из двух вопросов, предлагаемых преподавателем студенту. Студент не знает ответов на восемь вопросов из тех сорока, которые могут быть предложены. Какова вероятность, что студент сдаст коллоквиум?
Решение.
Пусть ![]() и
и ![]() - события,
заключающиеся в том, что студент знает ответы соответственно на первый и второй
вопросы. Тогда
- события,
заключающиеся в том, что студент знает ответы соответственно на первый и второй
вопросы. Тогда ![]() и
и ![]() - студент не знает ответов на эти вопросы. Пусть, далее, событие
- студент не знает ответов на эти вопросы. Пусть, далее, событие ![]() означает, что студент сдал коллоквиум, т.
е. ответил хотя бы на один вопрос. Тогда
означает, что студент сдал коллоквиум, т.
е. ответил хотя бы на один вопрос. Тогда ![]() - студент не сдал коллоквиум, т. е. не ответил на оба вопроса. Очевидно,
что
- студент не сдал коллоквиум, т. е. не ответил на оба вопроса. Очевидно,
что ![]() =
=![]()
![]() и
и 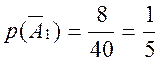 .
Вероятность того, что студент не знает ответа на второй вопрос при условии, что
он не ответил и на первый вопрос, равна
.
Вероятность того, что студент не знает ответа на второй вопрос при условии, что
он не ответил и на первый вопрос, равна 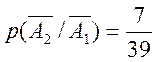 (так
как из 39 вопросов студент уже не знает только 7).
(так
как из 39 вопросов студент уже не знает только 7).
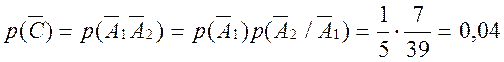 .
.
Отсюда,
![]() .
.
Ответ:
![]() .
.
Пример 14. Каждый француз, в среднем, ежегодно съедает около 20 кг сыра. Оценить вероятность того, что некий француз употребит за год более 30 кг сыра.
Решение.
Для решения используем первое неравенство Чебышева: если случайная величина ![]() неотрицательна
и имеет математическое ожидание, то
неотрицательна
и имеет математическое ожидание, то 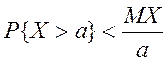 .
.
Учитывая, что по условию ![]() ,
, ![]() . Получаем:
. Получаем: ![]() .
.
Ответ: ![]() .
.
Пример 15. Среднее количество выпадающих в течение года в некоторой местности осадков составляет 50см. Оценить вероятность того, что в этой местности осадков выпадет не более 150см.
Решение.
События, состоящие в том, что количество осадков,
выпадающих в некоторой местности в течение года, будет более и не более 150 мм
- противоположные. Поэтому, используем
первое неравенство Чебышева: если
случайная величина ![]() неотрицательна и имеет
математическое ожидание, то
неотрицательна и имеет
математическое ожидание, то 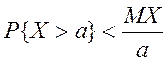 . По условию
. По условию ![]() получаем:
получаем:
![]() .
.
Ответ: ![]() .
.
Пример 16. У туриста, находящегося в Таиланде, в 14:00 намечается три мероприятия: либо пойти на обед, который обойдётся ему в среднем в $15, но не более $25, либо пойти на экскурсию, средней стоимостью в $9 и не более $12, либо прогуляться на водном мотоцикле, стоимостью от $28 до $30 в час. Оценить вероятность реализации одного из первых двух мероприятий.
Решение.
Все три мероприятия,
которые турист может реализовать в 14.00 несовместные. Поэтому вероятность
осуществления двух первых событий равна сумме их вероятностей, оцененных с
помощью первого неравенства Чебышева: если случайная
величина ![]() неотрицательна и имеет математическое
ожидание, то
неотрицательна и имеет математическое
ожидание, то 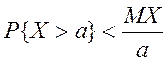 . Если по
условию
. Если по
условию
![]()
![]() ,
, ![]()
![]() .
.
Ответ: ![]() .
.
Пример 17. Вероятность того, что аккумулятор останется исправным после 1000 часов работы, равна 0,4. Какова вероятность того, что из 8 работающих аккумуляторов останутся исправными после 1000 часов работы 6?
Решение.
По условию ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Необходимо найти
. Необходимо найти ![]() .
.
Так
как вероятность события «аккумулятор исправен после 1000 часов работы»
постоянна для всех аккумуляторов, проходящих испытания, то применима формула
Бернулли: Искомая вероятность: 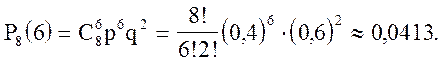
Ответ:
![]()
Пример 18. Фабрика выпускает 3000 футболок. Вероятность высокого качества футболки равна 0,35. Найти вероятность того, что высокого качества будут 1060 футболок.
Решение.
По условию ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Необходимо найти
. Необходимо найти ![]() .
Воспользуемся локальной предельной теоремой Муавра-Лапласа:
.
Воспользуемся локальной предельной теоремой Муавра-Лапласа: 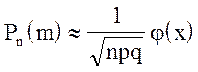 , где
, где 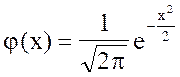 ,
причем значение аргумента находят по формуле:
,
причем значение аргумента находят по формуле: 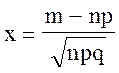 .
.
Находим последовательно:
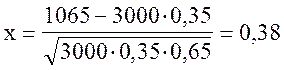 .
.
![]() .
.
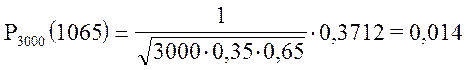 .
.
Ответ: ![]() .
.
Пример 19. Производят исследование точности прицела ракет. Вероятность достижения цели ракетой равна 0,9. Какова вероятность того, что из 1000 пущенных ракет поразят цель от 888 до 912?
Решение.
По условию ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Необходимо найти
.
Необходимо найти ![]() . Воспользуемся интегральной
теоремой Лапласа. Найдем
. Воспользуемся интегральной
теоремой Лапласа. Найдем ![]() :
:
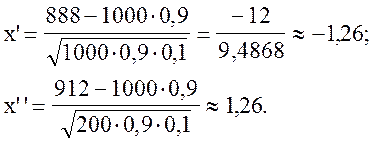
![]() .
.
По таблицам плотности нормального закона интеграла вероятности найдем
![]() .
.
Искомая вероятность
![]()
Ответ:
![]()
Пример 20. Вероятность того, что при включении телевизора в вечернее время по одному из каналов будет идти комедия, равна 0,01. Какова вероятность того, что если будем включать телевизор каждый вечер один раз в течении 200 дней, комедию увидим 3 раза?
Решение.
По условию ![]() ,
, ![]() ,
, ![]() .
Необходимо найти
.
Необходимо найти ![]() . Так как испытания «каждый
вечер» независимы, вероятность мала, число независимых испытаний велико,
поэтому воспользуемся теоремой Пуассона: если при
. Так как испытания «каждый
вечер» независимы, вероятность мала, число независимых испытаний велико,
поэтому воспользуемся теоремой Пуассона: если при ![]() независимых
испытаниях некоторое событие происходит с вероятностью
независимых
испытаниях некоторое событие происходит с вероятностью ![]() близкой
к нулю, то при достаточно большом
близкой
к нулю, то при достаточно большом ![]() вероятность
осуществления события
вероятность
осуществления события ![]() раз приближенно равна:
раз приближенно равна: 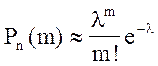 , где
, где ![]() .
.
Найдем
l: ![]() .
Искомая вероятность
.
Искомая вероятность 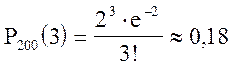 .
.
Ответ:
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.