






Практичне заняття №4
“Похідна в даному напрямку. Градієнт функції. Диференціювання неявних функцій. Дотична площина й нормаль до поверхні”
Похідна в даному напрямку. Градієнт функції.
Похідною функції ![]() в крапці
в крапці ![]() в
напрямку вектора
в
напрямку вектора ![]() називається межа
називається межа
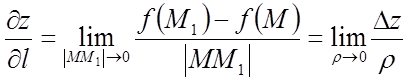 ,
,
де ![]() .
.
Якщо функція ![]() диференціюєма, то похідна в даному
напрямку обчислюється по формулі
диференціюєма, то похідна в даному
напрямку обчислюється по формулі
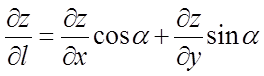
де α – кут, утворений вектором I з віссю Ох.
У випадку функції
трьох перемінних ![]() похідна в даному напрямку
визначається аналогічно. Відповідна формула має вигляд
похідна в даному напрямку
визначається аналогічно. Відповідна формула має вигляд
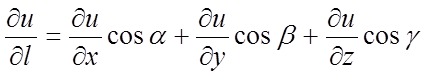 ,
,
де ![]() – направляючі косинуси
вектора I.
– направляючі косинуси
вектора I.
Градієнтом функції ![]() в крапці
в крапці ![]() називається
вектор, що виходить із крапки М и то, що має своїми координатами
приватні похідні функції z:
називається
вектор, що виходить із крапки М и то, що має своїми координатами
приватні похідні функції z:
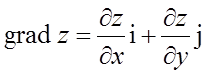
Градієнт функції і похідна в напрямку вектора I зв'язані формулою
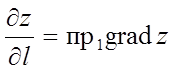 .
.
Градієнт указує
напрямок найшвидшого росту функції в даній крапці. Похідна 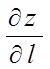 в напрямку градієнта має найбільше
значення, рівне
в напрямку градієнта має найбільше
значення, рівне
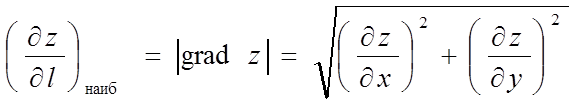
У випадку функції ![]() градієнт функції дорівнює
градієнт функції дорівнює
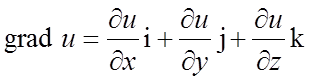 .
.
Приклад 1.
Знайти похідну
функції ![]() в крапці М(1, 1) у напрямку вектора
I, що складає кут α = 60° з позитивним напрямком осі Ох.
в крапці М(1, 1) у напрямку вектора
I, що складає кут α = 60° з позитивним напрямком осі Ох.
Рішення.
Знайдемо значення приватних похідних у крапці М:
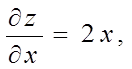
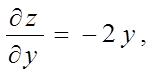
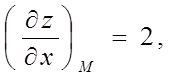
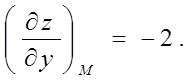
Тому що ![]() ,
, ![]() , то
, то
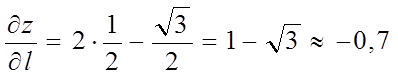 .
.
Приклад 2.
Знайти похідну функції ![]() в крапці М(3, 4) у напрямку
градієнта функції z.
в крапці М(3, 4) у напрямку
градієнта функції z.
Рішення.
Тут вектор I збігається з градієнтом
функції ![]() в крапці М(3, 4) і дорівнює
в крапці М(3, 4) і дорівнює
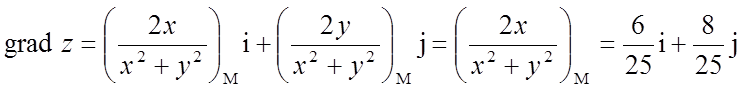 .
.
Отже,
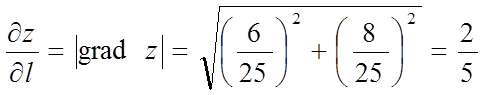 .
.
Приклад 3.
Знайти величину і напрямок градієнта
функції ![]() в крапці
в крапці ![]() .
.
Рішення.
Знайдемо приватні похідні
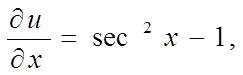
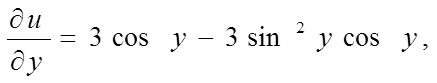
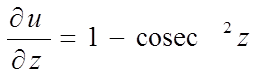
і обчислимо їх значення в крапці ![]() :
:
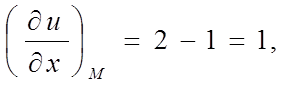
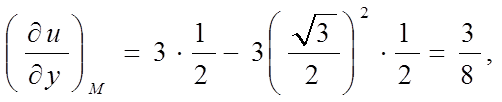
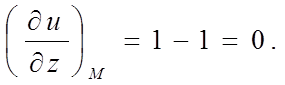
Отже,
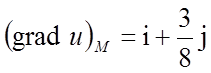 ;
; 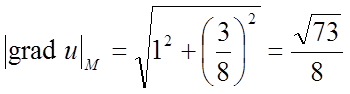 ;
;
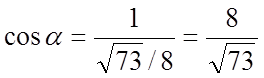 ;
; 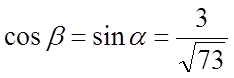 .
.
Диференціювання неявних функцій.
Похідна неявної
функції ![]() заданої за допомогою рівняння
заданої за допомогою рівняння ![]() , де
, де ![]() –
диференціюєма функція перемінних х и у, може бути обчислена по
формулі
–
диференціюєма функція перемінних х и у, може бути обчислена по
формулі
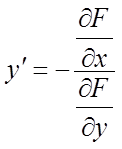
за умови, що 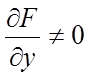 .
.
Похідні вищих порядків неявної функції можна знайти послідовним диференціюванням зазначеної формули, розглядаючи при цьому у як функцію від х.
Аналогічно,
приватні похідні неявної функції двох перемінних ![]() заданої
за допомогою рівняння
заданої
за допомогою рівняння ![]() , де
, де ![]() –
диференціюєма функція перемінних х, у и z, можуть бути
обчислені по формулах
–
диференціюєма функція перемінних х, у и z, можуть бути
обчислені по формулах
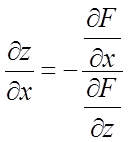 ,
, 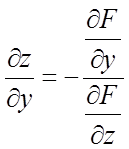
за умови, що 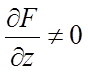 .
.
Приклад 4.
![]() . Знайти
. Знайти ![]() і
і ![]()
Рішення.
Тут ![]() .
Знайдемо
.
Знайдемо 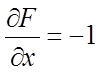 ,
, 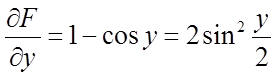 , відкіля
, відкіля
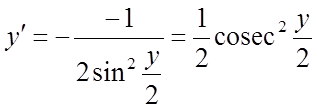 .
.
Знайдемо другу похідну:
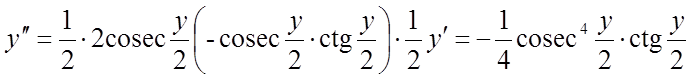 .
.
Приклад 5.
![]() . Знайти
. Знайти ![]() ,
, ![]() .
.
Рішення.
Тут ![]() .
Знаходимо
.
Знаходимо 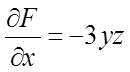 ,
, 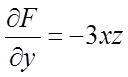 ,
, 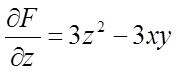 . Тоді
. Тоді
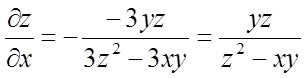 ;
; 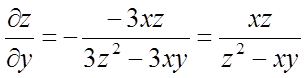 .
.
Приклад 6.
![]() . Знайти
. Знайти ![]() .
.
Рішення.
Як відомо, 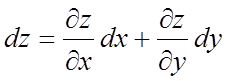 ,
тому знайдемо спочатку
,
тому знайдемо спочатку ![]() і
і ![]() :
:
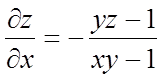 ,
, 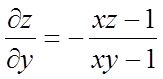 .
.
Отже,
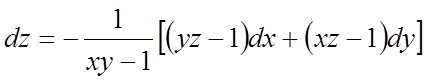 .
.
Дотична площина і нормаль до поверхні.
Дотичною площиною до поверхні в крапці М називається площина, що містить у собі всі дотичні до кривих, проведених на поверхні через крапку М.
Нормаллю до поверхні називається пряма, що проходить через крапку торкання М и перпендикулярна дотичній площини.
Якщо поверхня
задана рівнянням ![]() , то рівняння дотичної площини в
крапці
, то рівняння дотичної площини в
крапці ![]() поверхні має вигляд
поверхні має вигляд
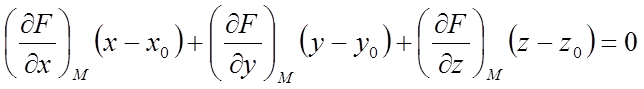 ,
,
де 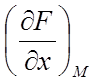 ,
, 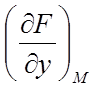 ,
, 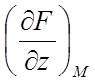 –
значення приватних похідних у крапці М, а х, у, z – поточні
координати крапки дотичної площини.
–
значення приватних похідних у крапці М, а х, у, z – поточні
координати крапки дотичної площини.
Рівняння нормалі до поверхні в крапці М записуються у виді
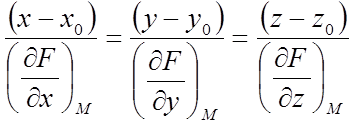 .
.
Тут х, у, z – поточні координати крапки нормалі.
Якщо ж рівняння
поверхні задане явно ![]() , то рівняння дотичної площини в
крапці
, то рівняння дотичної площини в
крапці ![]() записується у виді
записується у виді
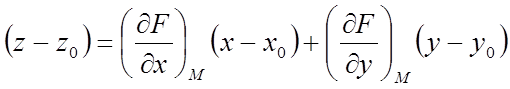 ,
,
а рівняння нормалі – у виді
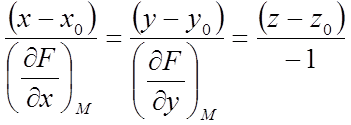 .
.
Приклад 7.
Дано поверхню ![]() .
Скласти рівняння дотичної площини і рівняння нормалі до поверхні в крапці
.
Скласти рівняння дотичної площини і рівняння нормалі до поверхні в крапці ![]() .
.
Рішення.
Знайдемо приватні
похідні 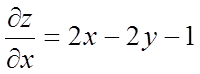 й
й 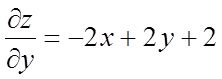 і їх
значення в крапці
і їх
значення в крапці ![]() :
: 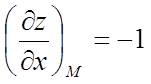 ,
, 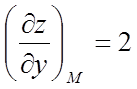 .
.
Рівняння дотичної площини:
![]() , або
, або ![]() .
.
Рівняння нормалі:
![]() .
.
Приклад 8.
До поверхні ![]() провести
дотичні площини, рівнобіжні площини
провести
дотичні площини, рівнобіжні площини ![]() .
.
Рішення.
Тут ![]() .
Знайдемо приватні похідні:
.
Знайдемо приватні похідні:
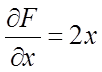 ,
, 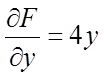 ,
, 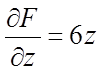 .
.
З умови
паралельності дотичної площини і даної площини випливає, що ![]() , або
, або ![]() .
Приєднавши до цих рівнянь рівняння поверхні
.
Приєднавши до цих рівнянь рівняння поверхні ![]() ,
знайдемо координати крапок торкання:
,
знайдемо координати крапок торкання: ![]() і
і ![]() .
.
Отже, рівняння дотичних площин мають вигляд
![]() ,
,
т. е.
![]() и.
и.![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.