Практическое занятие 1.
Тема: Постановка задачи теории управления.
Реальные системы управления, как правило, достаточно сложны. Приведенные ниже примеры используются в основном для иллюстрации задач теории управления. Поэтому рассматриваемые системы управления отличаются максимальной простотой и наглядностью.
Пример 1.1.
Предположим, что некоторая материальная точка ![]() массы
массы ![]() может двигаться только по прямой линии,
вдоль которой на точку действует сила
может двигаться только по прямой линии,
вдоль которой на точку действует сила ![]() .
Положение точки
.
Положение точки ![]() характеризуется координатой
характеризуется координатой ![]() (рис. 1.1).
(рис. 1.1).
Пусть известны граничные условия, т.е. положение точки
![]() в начальный
в начальный ![]() и
конечный
и
конечный ![]() моменты времени
моменты времени ![]() ,
соответственно
,
соответственно
![]() ,
, ![]() ,
(1.1)
,
(1.1)
а
также начальная и конечная скорости точки ![]()
![]() ,
, ![]() .
(1.2)
.
(1.2)
Если пренебречь силами сопротивления движению, то
согласно второму закону Ньютона уравнение движения точки ![]() можно представить в следующем виде
можно представить в следующем виде
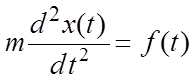 , или
, или 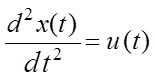 ,
(1.3)
,
(1.3)
где
![]() .
.
При решении задач управления принято пользоваться понятиями фазового пространства и фазовых координат.
Введем следующие обозначения ![]() и
и
![]() . Тогда уравнение (1.3) можно записать в
виде системы дифференциальных уравнений первого порядка
. Тогда уравнение (1.3) можно записать в
виде системы дифференциальных уравнений первого порядка
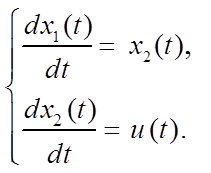 (1.4)
(1.4)
Система дифференциальных уравнений первого порядка, разрешенных относительно производных, называется нормальной. Так что система (1.4) представлена в нормальной форме.
Переменные ![]() и
и ![]() являются фазовыми координатами двухмерного
фазового пространства (фазовой плоскости). Время
являются фазовыми координатами двухмерного
фазового пространства (фазовой плоскости). Время ![]() в явном виде не входит. При изменении
в явном виде не входит. При изменении ![]() изображающая точка
изображающая точка ![]() перемещается
по фазовой плоскости, прочерчивая линию, которая называется фазовой траекторией
(рис.1.2).
перемещается
по фазовой плоскости, прочерчивая линию, которая называется фазовой траекторией
(рис.1.2).
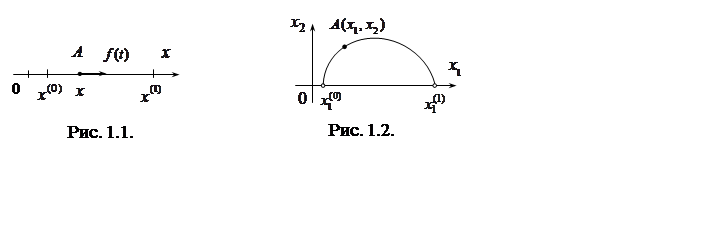 |
Фазовые координаты дают возможность записать граничные условия (1.1) и (1.2) в следующем виде
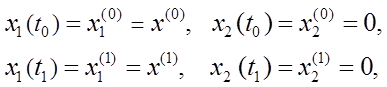 (1.5)
(1.5)
Фазовые траектории по существу являются графической интерпретацией решения системы дифференциальных уравнений (1.4) с краевыми условиями (1.5).
Задание граничных условий (1.5) и выбор возможного
управления ![]() определяют единственным образом
непрерывное движение или фазовую траекторию
определяют единственным образом
непрерывное движение или фазовую траекторию ![]() .
Вектор
.
Вектор ![]() называется фазовым вектором. Показателем
качества процесса управления (или критерием оптимальности) является числовое
значение некоторого функционала
называется фазовым вектором. Показателем
качества процесса управления (или критерием оптимальности) является числовое
значение некоторого функционала ![]() .
.
На основе (1.4) и (1.5) можно сформулировать несколько
задач оптимального управления движением точки ![]() ,
которые будут отличаться критериями оптимальности и видом ограничений.
,
которые будут отличаться критериями оптимальности и видом ограничений.
Задача оптимального быстродействия. В этом
случае критерием оптимальности является время переходного процесса ![]() , т.е.
, т.е. ![]() – нефиксированная
величина и функционал имеет вид
– нефиксированная
величина и функционал имеет вид
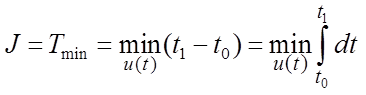 . (1.6)
. (1.6)
Необходимо
найти оптимальные управление ![]() и траекторию
и траекторию ![]() , удовлетворяющие (1.4), (1.5) и
доставляющие минимум функционалу (1.6). При этом могут быть дополнительные
условия, например, ограничение на управление
, удовлетворяющие (1.4), (1.5) и
доставляющие минимум функционалу (1.6). При этом могут быть дополнительные
условия, например, ограничение на управление ![]() .
.
Задача оптимальной производительности. В этом случае критерием оптимальности является
наибольшее расстояние ![]() за определенное время
за определенное время ![]() , т.е. функционал имеет вид
, т.е. функционал имеет вид
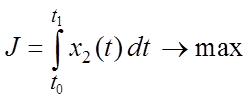 . (1.7)
. (1.7)
Необходимо
найти оптимальные процесс управления ![]() и траекторию
и траекторию ![]() , удовлетворяющие (1.4), начальным условиям
, удовлетворяющие (1.4), начальным условиям
![]() ,
, ![]() ,
конечным условиям
,
конечным условиям ![]() и доставляющие максимум
функционалу (1.7). При этом могут быть дополнительные условия, например,
ограничение на управление
и доставляющие максимум
функционалу (1.7). При этом могут быть дополнительные условия, например,
ограничение на управление ![]() .
.
Задача оптимальной экономичности. В этом случае критерием оптимальности является расход энергии за определенное время. Функционал имеет вид
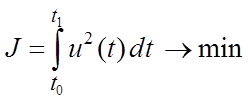 .
(1.8)
.
(1.8)
Необходимо
найти оптимальные процесс управления ![]() и траекторию
и траекторию ![]() , удовлетворяющие системе (1.4), начальным
условиям
, удовлетворяющие системе (1.4), начальным
условиям ![]() ,
, ![]() ,
конечным условиям
,
конечным условиям ![]() ,
, ![]() и
доставляющие минимум функционалу (1.8). При этом могут быть дополнительные условия,
например, ограничение на управление
и
доставляющие минимум функционалу (1.8). При этом могут быть дополнительные условия,
например, ограничение на управление ![]() .
.
Можно, варьируя условия, поставить еще ряд задач.
Пример 1.2.
Движение плоского маятника, подвешенного к точке опоры при помощи жесткого невесомого стержня (рис. 1.3), описывается уравнением
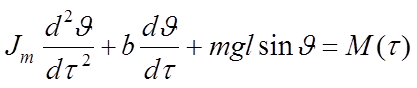 ,
(1.9)
,
(1.9)
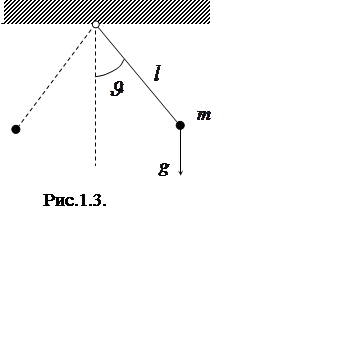 где
где ![]() – длина жесткого стержня маятника,
– длина жесткого стержня маятника, ![]() – масса, сосредоточенная в конце стержня,
– масса, сосредоточенная в конце стержня, 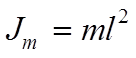 – момент инерции,
– момент инерции, ![]() – гравитационная постоянная (ускорение силы тяжести),
– гравитационная постоянная (ускорение силы тяжести), ![]() –коэффициент демпфирования,
–коэффициент демпфирования, ![]() – время,
– время,
![]() – внешний
управляющий момент,
– внешний
управляющий момент, ![]() – угол отклонения стержня от
точки устойчивого равновесия.
– угол отклонения стержня от
точки устойчивого равновесия.
Если сделать замену переменной 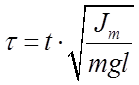 , то уравнение (1.9) можно привести к виду
, то уравнение (1.9) можно привести к виду
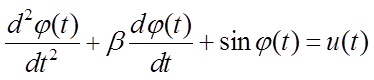 ,
(1.10)
,
(1.10)
где
![]() ,
, 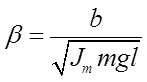 ,
, 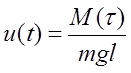 .
.
Введем следующие обозначения: ![]() – угол отклонения маятника,
– угол отклонения маятника, 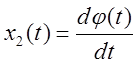 – скорость изменения угла отклонения
маятника. Тогда уравнение (1.10) запишется в виде эквивалентной системы двух
уравнений первого порядка
– скорость изменения угла отклонения
маятника. Тогда уравнение (1.10) запишется в виде эквивалентной системы двух
уравнений первого порядка
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.