Принцип максимума Понтрягина: Практическое занятие № 7

Практическое занятие  7.

Тема: Принцип максимума Понтрягина.

Цель занятия : ознакомление с методикой решения задач оптимального управления с ограниченными управлениями на основании принципа максимума Понтрягина.

При решении задач с помощью принципа максимума удобно придерживаться следующего алгоритма:

1. Записываем уравнения объекта в виде системы уравнений первого порядка, не забыв уравнение для функционала:

.

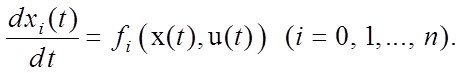2. Составляем функцию Гамильтона :

.

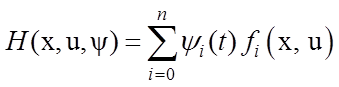3. Определяем значение , максимизирующее функцию , из системы уравнений

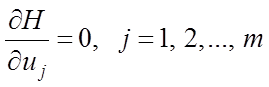.                                       (7.1)

Возможно, что максимум  достигается на границе допустимой области управлений, тогда для некоторых  равенство (7.1) может не выполняться при ненулевой функции .

В уравнениях (7.1) для определения 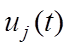 содержится  неизвестных:  функций ,  функций  и  функций . Для их определения имеются  уравнений (7.1),  уравнений исходной системы и осталось составить еще  уравнений для функций .

4. Составляем уравнения для определения

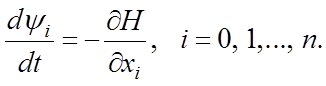                                  (7.2)

Из совместного решения названных  уравнений находим оптимальное управление .

Особенностью принципа максимума является то, что вариационная задача нахождения функции , минимизирующей функционал , заменена более простой задачей математического анализа нахождения параметра , доставляющего максимум вспомогательной функции . Отсюда, как было сказано ранее, и название метода – принцип максимума.

Напомним, что, используя теорему о максимуме, мы отыскиваем решение не в классе кусочно-гладких функций, а в более широком классе кусочно-непрерывных функций.

Пример 6.1.

Система управления описывается следующими дифференциальными уравнениями:

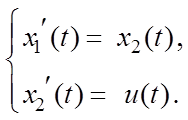                                            (7.3)

Требуется определить управление , обеспечивающее быстрейший перевод системы из состояния  в начало координат  при условии, что управление должно удовлетворять ограничению .

Решение.

Функционал процесса управления: .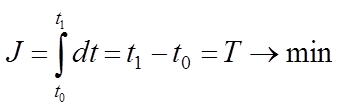

Таким образом, полная исходная система уравнений объекта будет иметь следующий вид:

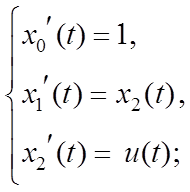
Составляем функцию Гамильтона:

.

Из последнего выражения видно, что  достигнет максимального значения, если

.

Для вспомогательных функций  и  составим систему сопряженных уравнений (7.2)

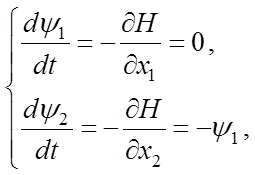
решая которую, найдем , . Следовательно, оптимальное управление имеет вид

,

т.е. управление с течением времени не более чем один раз меняет знак.

Поскольку линейная функция  на любом промежутке  меняет знак не более одного раза, то какова бы ни была начальная точка , соответствующее оптимальное управление является кусочно-постоянной функцией, принимающей значение  или  и имеющей не более двух интервалов постоянства.

Для отрезка времени, на котором  из системы (7.3) находим уравнение

,

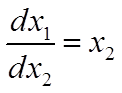после интегрирования которого получим семейство кривых

,

где  – произвольная постоянная интегрирования.

По этим кривым происходит движение изображающей точки системы при . На рис. 7.1 эти траектории изображены с указанием направления движения (из второго уравнения системы (7.3) видно, что с возрастанием  координата  возрастает, поэтому движение изображающей точки происходит снизу вверх).

Интегрируя систему уравнений (7.3) при  по аналогии с предыдущим, получим семейство траекторий (рис. 7.2)   .

 

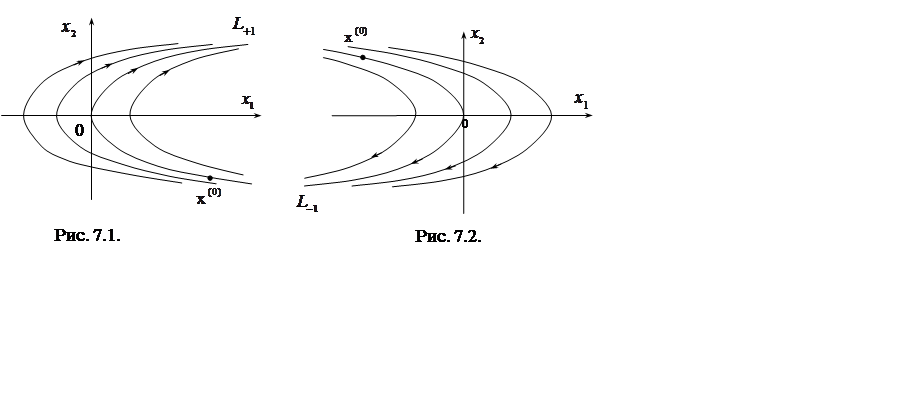В каждом из семейств траекторий имеется лишь одна полудуга параболы, по которой изображающая точка может приблизиться к началу координат. На рисунках эти дуги обозначены через  и  (индексы равны значениям управлений, при которых происходит указанное движение).

Если изображающая точка  в начальный момент времени лежит на дуге , то оптимальное управление , приводящее систему из точки  в начало координат за минимальное время, равно , а траектория системы совпадает с некоторым куском линии  (рис. 7.1). Если точка  лежит на дуге , то  и траектория системы расположена на  (рис. 7.2). Только в этих двух случаях оптимальное управление постоянно (в смысле знака) в течение всего времени движения. Во всех других случаях расположения начальной точки  на плоскости  оптимальное управление  меняет свое значение либо с  на  , либо с  на . Оптимальные траектории в этих случаях также состоят из двух частей – одна часть совпадает с куском параболы семейства  (если вначале ) , по которому движение происходит до момента пересечения ее с линией , а другая часть совпадает с куском линии  от упомянутой точки пересечения до начала координат. Аналогичный переход фазовой точки происходит на линию , если вначале . На рис. 7.3 изображено все семейство фазовых траекторий рассматриваемой системы.

 

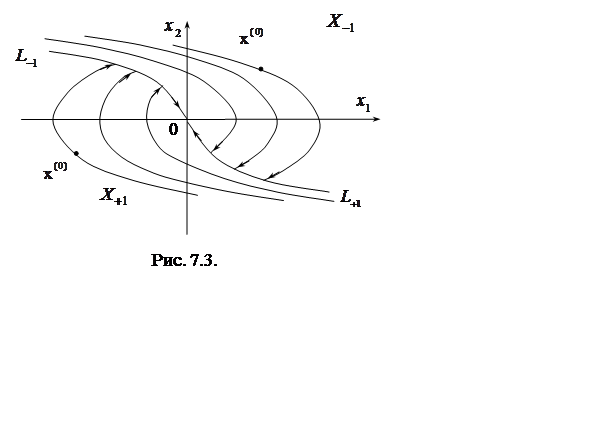Как видим, фазовая плоскость  разделяется линиями  и  на две части:  и . Если точка 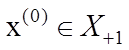  () , то фазовая точка должна двигаться под воздействием оптимального управления  () до линии  (), после чего ее движение происходит по этой линии под воздействием управления  (). Отсюда видно, что на линии  происходит переключение знака управления. Благодаря такому свойству, эту линию называют линией переключения.

Пример 7.2.

Пусть система управления описывается уравнениями вида

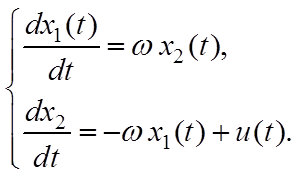                                         (7.4)

Это система с мнимыми собственными значениями ,  и с одним входным управлением (гармонический осциллятор с одним входом).