Частотные характеристики систем управления

Лекция  3.

Тема:  Частотные характеристики систем

управления.

План:

1.  Преобразование Фурье.

2.  Частотные характеристики линейных систем управления.

3.  Характеристики систем при различных соединениях звеньев.

1. Рассмотрим линейную систему управления с постоянными коэффициентами, описывающуюся уравнением

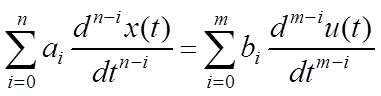,                               (3.1)

и до момента  подачи управляющего сигнала находящуюся в покое, т.е. при нулевых начальных условиях

      .                          (3.2)

Преобразование Фурье – одно из интегральных преобразований, тесно связанное с преобразованием Лапласа.

Определение 3.1. Функция  действительного аргумента  называется оригиналом по Фурье, если она однозначна, непрерывна или имеет конечное число точек разрыва первого рода и абсолютно интегрируема на всей числовой оси.

Определение 3.2. Изображением по Фурье функции-оригинала  называется функция  действительного аргумента , которая определяется интегралом

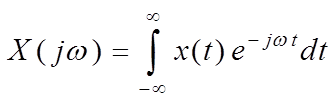.                                   (3.3)

Функция-оригинал по Фурье удовлетворяет следующему соотношению:

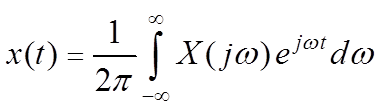.                           (3.4)

Соотношения (3.3) и (3.4) называются соответственно прямым и обратным преобразованиями Фурье.

Если функция  для всех , то прямое преобразование Фурье принимает вид

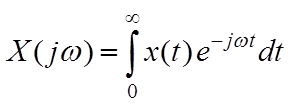,                                  (3.5)

которое формально с точностью до обозначений совпадает с прямым преобразованием Лапласа при условии, что .

Применив преобразование Фурье (3.5) к линейной одномерной системе управления, которая определяется уравнением (3.1) и начальными условиями (3.2), получим

,                      (3.6)

где  и  – изображенияФурье функций и ; и соответствующие многочлены

;

.

Равенство (3.6) можно записать в виде

.

2. Функция  называется комплексной частотной характеристикой системы, или частотной передаточной функцией, или амплитудно-фазовой характеристикой. Частотная передаточная функция  есть изображение Фурье импульсной переходной функции . Как видим, функция , т. е. комплексная частотная характеристика совпадает с передаточной функцией, в которую вместо переменной  подставлена переменная .

Комплексную частотную характеристику можно представить в одной из двух форм

;      .

Функция  называется амплитудной частотной характеристикой системы,  – фазовой частотной характеристикой системы,  – действительной частотной характеристикой системы (не путать с изображением  функции управления ), – мнимой частотной характеристикой системы.

Комплексная частотная характеристика  представляет собой отношение установившейся реакции  системы к данному входному сигналу вида 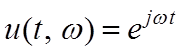 . Тогда амплитудная частотная характеристика  есть отношение амплитуды установившегося выходного гармонического сигнала к амплитуде входного гармонического сигнала с частотой  . Аналогично  – разность фаз выходного и входного гармонических сигналов.

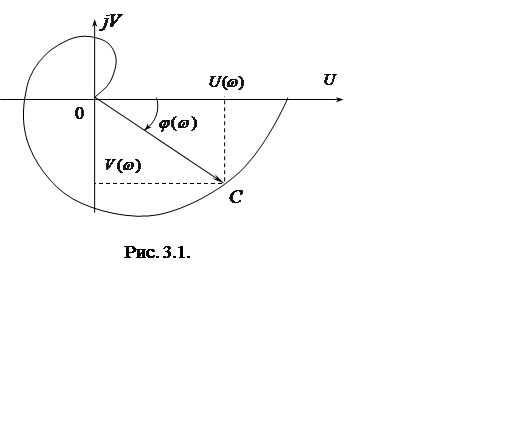
На комплексной плоскости (рис. 3.1) частотная передаточная функция  определяется вектором , длина которого равна , и аргументом  (углом, образованным этим вектором с положительным направлением действительной полуоси). Кривую, которую описывает конец этого вектора при изменении частоты от 0 до  (иногда от  до ), называют амплитудно-фазовой частотной характеристикой (АФЧХ).

Частотную передаточную функцию называют также амплитудно-фазовой частотной функцией. Ее действительную часть  и мнимую часть  называют соответственно вещественной и мнимой частотной функцией. График вещественной частотной функции (кривая зависимости ) – вещественной частотной характеристикой, а график мнимой частотной функции  – мнимой частотной характеристикой.

Модуль 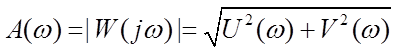 называют амплитудной частотной функцией, ее график – амплитудной частотной характеристикой.

Аргумент  называют фазовой частотной функцией, ее график – фазовой частотной характеристикой.

Вообще говоря, действительная  и мнимая  частотные характеристики находятся в определенной зависимости. Для достаточно широкого класса систем такая зависимость оказывается однозначной. В этом случае системы называются минимально-фазовыми. Для минимально-фазовых систем справедливы соотношения

,       ,

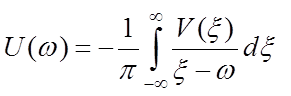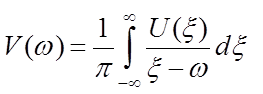где под интегралами следует понимать их главные значения по Коши.

Амплитудная  и фазовая  частотные характеристики  удовлетворяют аналогичным равенствам, а именно:

,         .

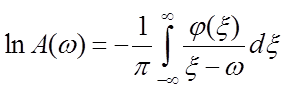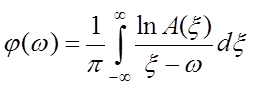Кроме перечисленных частотных характеристик при исследовании систем управления используют так называемую логарифмическую частотную характеристику (ЛЧХ), которая представляет собой натуральный логарифм комплексной частотной характеристики

.

В практике используются логарифмическая амплитудная частотная функция следующего вида:

.

График зависимости логарифмической амплитудной частотной функции  от логарифма частоты  называют логарифмической амплитудной частотной характеристикой (ЛАЧХ). При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе: на отметке, соответствующей значению , пишут само значение , а не значение , а по оси ординат –  значение .

3. Отдельные звенья систем управления можно соединить друг с другом различными способами. Рассмотрим три способа соединения: последовательное, параллельное и антипараллельное.

Интерес представляет задача об определении импульсной переходной функции и передаточной функции той части системы, которая состоит из  звеньев, если соответствующие характеристики отдельных звеньев известны. Все другие характеристики можно определить на основании приведенных выше формул по этим двум функциям.