Управляемость в линейных системах

Лекция  4.

Тема:  Управляемость в линейных системах .

План:

1.  Полная и неполная управляемость многомерной системой.

2.  Критерий управляемости.

3.  Грамиан управляемости стационарной системы.

4.  Матрица управляемости – критерий управляемости стационарной системы.

Рассмотрим задачу об управляемости многомерными системами, функционирование которых описывается нормальной системой линейных дифференциальных уравнений. Система уравнений в матричной форме имеет следующий вид:

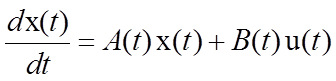,                                 (4.1)

где  – векторы-столбцы размерности  и  соответственно;  – матрицы размерности  и  соответственно.

Определение 4.1. Система (4.1) называется вполне управляемой, если для двух произвольных точек  и  области допустимых решений фазового пространства  и двух произвольных значений  и  аргумента  существует такая функция управления   , при которой решение уравнения (4.1) удовлетворяет условиям  и .

Начнем с простейшего случая, когда матрица  в уравнении системы (4.1) равна нулевой матрице. Тогда динамика системы задана уравнением

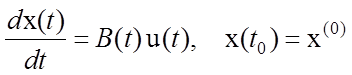.                        (4.2)

Предположим, что  и  известны, и поставим задачу выбора такого управления , которое обеспечивало бы в момент времени  при  выполнение условия .

Интегрирование уравнения движения системы (4.2) дает

.

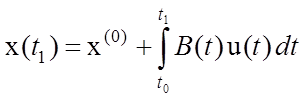Заметим, что выражение

                                    (4.3)

можно рассматривать как линейное преобразование, которое ставит в соответствие каждому элементу  гильбертова пространства  элемент пространства . Формально

,    .

Поскольку нужно выбрать управление , которое удовлетворяло бы условию

,

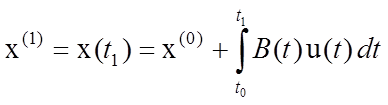то, очевидно, если  лежит в области значений линейного преобразования , тогда желаемый перевод системы в  возможен. В противном случае – нет. Чтобы сформулировать эту задачу в общем виде, введем соответствующие определения.

Если  – матрица , составленная из непрерывных функций времени, определенных на интервале , то преобразование , определяемое формулой (4.3), является линейным преобразованием.

Говорят, что  принадлежит области значений этого преобразования, если существует элемент  в пространстве  такой, что

.

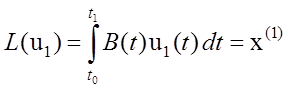Таким образом, чтобы проверить, является ли состояние управляемым, необходимо установить, принадлежит ли это состояние области значений оператора , преобразующего бесконечномерное пространство в конечномерное. Этот оператор не может быть записан с помощью конечной матрицы, и проверка названного условия затруднительна. К счастью, можно построить линейное преобразование, отображающее -мерное пространство в -мерное, область значений которого в точности совпадает с областью значений оператора . Это построение формулирует следующая лемма.

Лемма 4.1.. Вектор  размерности  лежит в области значений оператора

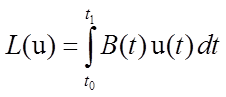
только тогда, когда он принадлежит области значений линейного преобразования

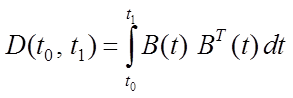                           (4.4)

Необходимость. Если  принадлежит области значений, т.е. , то существует вектор  такой, что . Определим  по формуле , тогда

.

Достаточность. Если  не лежит в области значений оператора , то существует вектор  такой, что 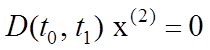 и скалярное произведение .

Можно указать, например, следующий способ построения вектора . Так как  – симметрический оператор, он расщепляет пространство  в прямую сумму

,

где  – ядро оператора . Пусть размерность ядра  отлична от нуля и пусть  – размерность области значений  ( – равно рангу матрицы ). Выберем в  базис  ,…, ,…,  такой, что векторы ,…,  лежат в области значений . Пусть  не лежит в области значений  и его представление в выбранном базисе имеет вид

,

причем  не все равны нулю. В качестве вектора  можно взять, например, вектор

.

Ясно, что , по предположению, и кроме того,

.

Предположим, что вектор  и одновременно является управляемым. Из управляемости  следует, что существует  такое, что

,

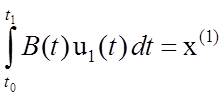тогда

,

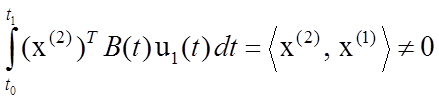но

.

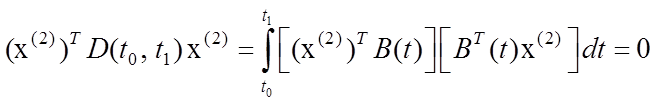Так как матрица  непрерывна, то из

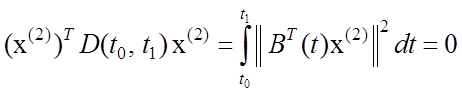
следует, что  при всех , а это противоречит условию

.

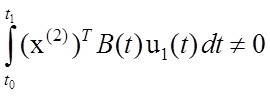Следствие. Управление , которое переводит систему (4.2) из состояния  при  в  при , существует тогда и только тогда, когда вектор  лежит в области значений линейного преобразования (4.4).

При этом одно из управлений, осуществляющее этот перевод, имеет вид , где  является любым решением уравнения

.

Доказательство. То, что управление  переводит состояние  в  проверено при доказательстве необходимости условий леммы 4.1. Обратно. Если управление , переводящее  в , существует, то вектор  принадлежит области значений линейного преобразования (4.3) в силу формулы Коши. Но по данной лемме вектор  принадлежит области значений этого преобразования тогда и только тогда , когда он лежит в области значений преобразования (4.4).

Перейдем теперь к линейной системе общего вида, когда . Здесь результат, аналогичный только что приведенному следствию леммы, формулируется в виде следующей теоремы.

Теорема 4.1. (критерий управляемости). Для линейной системы (4.1)

тогда и только тогда существует управление , которое переводит систему из состояния  при  в состояние  при , когда вектор  принадлежат области значений линейного преобразования

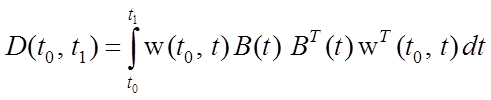.               (4.5)

Более того, если  – какое-либо решение уравнения

,

то , заданное формулой , является одним из управлений, обеспечивающих указанный переход.

Доказательство. Рассмотрим линейное преобразование уравнений системы управления с помощью замены переменной

 .

Тогда  и

.

По одному из свойств импульсной переходной матрицы :

,    .

Следовательно,

.

Умножая это равенство слева на , получим

.

Из предыдущей леммы известно, что множество значений, которые может принимать вектор , принадлежит области значений матрицы

.

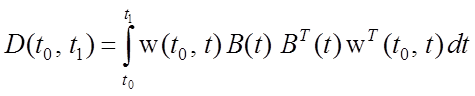Чтобы завершить желаемый переход потребуем, чтобы

.

Отсюда следует, что желаемое преобразование возможно тогда и только тогда, когда  лежит в области значений . Из следствия предыдущей леммы вытекает, что одно из управлений, обеспечивающее заданное преобразование системы, имеет вид

,

где  удовлетворяет равенству