Принцип максимума Понтрягина

Лекция  7

Тема:  Принцип максимума Понтрягина.

План:

1.  Особенности вывода принципа максимума.

2.  Постановка задачи оптимального управления. Теорема принципа максимума.

3.  Линейная система оптимального быстродействия. Вариант теоремы принципа максимума.

Напомним основные положения классического вариационного исчисления. Вариации функционалов считались непрерывными и линейными. Переменные, входящие в функционал или в уравнения связи ограничений не имели.

В практических задачах управления эти условия не всегда соблюдаются. Известно, что управляющие воздействия, которые входят в функционалы, могут быть кусочно-непрерывными, т.е. претерпевать разрывы первого рода. При некоторых условиях не только управляющие воздействия, но и координаты объекта, в частности производные, претерпевают разрывы. На фазовые координаты и управления, как правило, накладываются ограничения. Это соответствует тому, что координаты и управления могут изменяться в некоторых замкнутых областях и даже находиться на границах этих областей. А это значит, что нарушаются условия непрерывности.

Нарушение основных условий, на которых строится классическое вариационное исчисление, не позволяет решать широкий круг задач управления такими простыми способами, какие были описаны в гл.5. Эти трудности позволяет преодолеть принцип максимума.

Рассмотрим следующую постановку задачи управления. Пусть требуется перевести систему управления

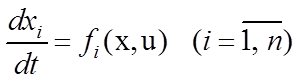,                                    (7.1)

где  – -мерный вектор фазового пространства и  – -мерный вектор управления, принадлежащий допустимому множеству кусочно-непрерывных функций замкнутого множества .

Ставится задача – найти управление , переводящее систему из состояния  в состояние  за время  и доставляющее минимум функционалу

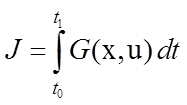.                                              (7.2)

В число фазовых координат включаем еще одну переменную , характеризующую текущее значение функционала (7.2), т.е.

.

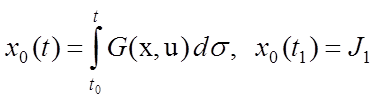Тогда систему (7.1) можно записать в виде

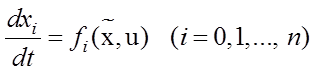,  где  ,        (7.3)

и ей будет соответствовать -мерное фазовое пространство.

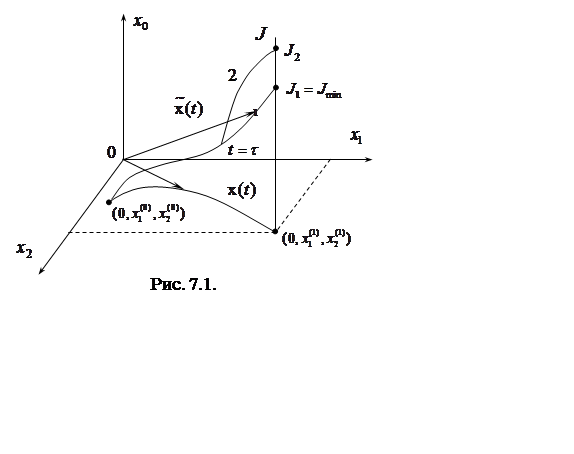
Рассмотрим геометрическую интерпретацию решения задачи (7.3). Для наглядности предположим, что .

 

Допустим, применено управление . Тогда  будет решением системы уравнений (7.3) при известных начальных условиях. Представим это решение графически в трехмерном фазовом пространстве (рис. 7.1). Начальное значение координат при : , , ; конечное значение при : , , . Проведем через точку  прямую , параллельную оси . Рассмотрим процесс управления, в результате которого получим две траектории. Одну траекторию  в плоскости ,  которая в момент  исходит из начальной точки  и в момент проходит через точку . Другую траекторию – в пространстве всех координат, которая исходит из начальной точки  и пересекает при  прямую . Так как на прямой  откладывается значение функционала , то фазовая траектория, пересекая прямую , даст значение функционала прямой  в момент . Для оптимального управления отрезок , т.е. должен иметь экстремальное значение. Рис. 7.1 дает графическое толкование решения системы (7.3).

Теперь найдем в пространстве  оптимальные траектории и соответствующие им управления. Для этого воспользуемся тем же приемом, которым пользовались в классическом вариационном исчислении. Однако здесь появляется следующая особенность. Кроме непрерывных управлений, нужно рассматривать и кусочно-непрерывные управления. Это значит, что вариация функции, и в частности , может быть большой из-за разрывов первого рода, поэтому будет большой и вариация функционала. В линейном плане такие вариации рассматривать уже нельзя и это сильно усложняет задачу.

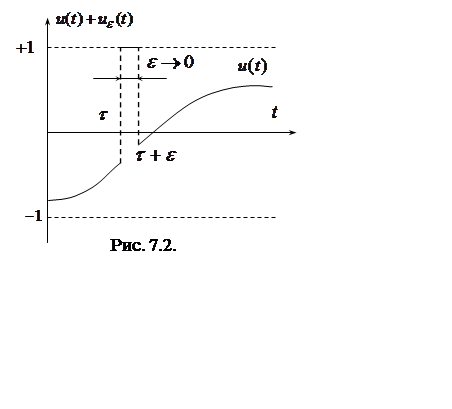
Однако авторами принципа максимума для доказательства всех теорем была использована так называемая игольчатая вариация или вариация Макшейна. Смысл ее состоит в следующем.

 

Как и при выводе уравнения Эйлера, к предполагаемой экстремали  добавляется вариация , вычисляется соответствующая первая вариация функционала , и из равенства этой вариации нулю выводятся необходимые условия оптимальности . Характерна форма вариации при выводе принципа максимума (рис. 7.2). Это импульс в момент  бесконечно малой длительности , но конечной, произвольной высоты . Единственное условие, которое наложено на величину  – это требования ограничения . Например, если , то . Вариация такого вида названа игольчатой вариацией. Так как импульс действует очень короткое время, то вариация функционала  будет малой. Поэтому приращения функционала можно рассматривать в линейном плане, а это упрощает задачу.

Важно отметить, что игольчатая вариация существенно отличается от вариаций, с помощью которых выводится уравнение Эйлера. Последние должны были представлять собой гладкие функции, в то время как игольчатая вариация является «скачкообразной». Использование скачкообразных вариаций позволяет включить в класс отыскиваемых экстремалей кусочно-непрерывные функции. А между тем, именно кусочно-непрерывные функции являются экстремалями во многих задачах оптимального управления.