Практичне заняття №13
Тема заняття: «Критерії стійкості: Гурвіца, Л’єнара-Шиппара, Михайлова»
I. Перевірка виконаного домашнього завдання.
II. Теоретичне опитування:
1. Навіщо потрібні критерії стійкості?
2. Сформулювати критерій стійкості Гурвіца.
3. Сформулювати критерій стійкості Л’єнара-Шиппара.
4. Сформулювати критерій стійкості Михайлова.
III. Розв'язання задач:
1.
При яких дійсних значеннях ![]() і
і ![]() дійсні частини корені многочлена
дійсні частини корені многочлена ![]() від’ємні?
від’ємні?
2.
Знайти всі значення параметрів ![]() і
і ![]() при яких система рівнянь
при яких система рівнянь 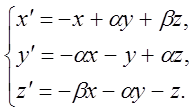 асимптотично стійка?
асимптотично стійка?
3.
При яких ![]() ,
, ![]() і
і ![]() розв'язання системи
розв'язання системи 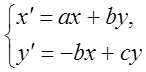 асимптотично стійке?
асимптотично стійке?
4.
При яких дійсних ![]() корені многочлена
корені многочлена ![]() мають від’ємні дійсні частини?
мають від’ємні дійсні частини?
5.
Досліджувати стійкість розв'язання системи 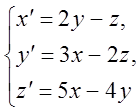
6. Використовуючи критерій Гурвіца дослідити на стійкість нульове розв'язання наступних рівнянь:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() ,
,
4) ![]() , 5)
, 5) ![]() .
.
7. При
яких значеннях ![]() і
і ![]() буде
стійко нульове розв'язання рівнянь:
буде
стійко нульове розв'язання рівнянь:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() ,
,
4) ![]() .
.
8. Використовуючи критерій Михайлова дослідити стійкість нульового розв'язання рівнянь:
1) ![]() , 2)
, 2) ![]() , 3)
, 3) ![]() .
.
9.
Довести, що якщо ![]() , то нульове розв'язання системи
рівнянь
, то нульове розв'язання системи
рівнянь 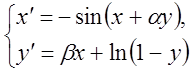 асимптотично стійке.
асимптотично стійке.
10. Дослідити на стійкість нульове розв'язання систем:
1) 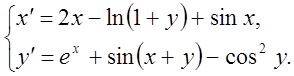 2)
2) 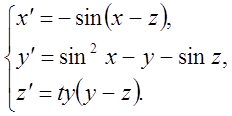 3)
3) 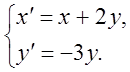
4) 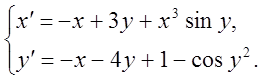 5)
5) 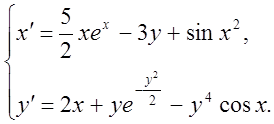
IV. Домашнє завдання:
1. Підготувати теоретичний матеріал по темі «Критерій стійкості по першому наближенню. Метод функцій Ляпунова».
2. Розв’язати вдома задачі, що залишилися
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.