Кореляційні функції. Похідна стаціонарної випадкової функції

Лабораторне заняття № 4

Задача 1. Нехай — нормальна стаціонарна випадкова функція, математичне чекання якої дорівнює нулеві. Довести що якщо

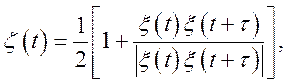 те

де  — нормована кореляційна функція .

Рішення. Користуючись тим, що  нормально, щільність імовірності другого порядку можемо представити у виді

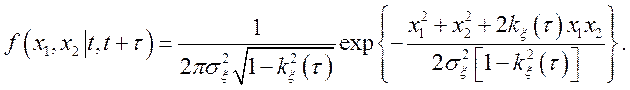
Шукане математичне чекання може бути представлене у виді

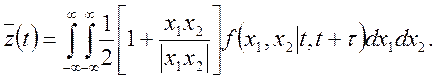
Тому що 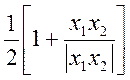 — тотожно дорівнює нулеві в тому випадку, коли знаки в ординат  і  різні, і дорівнює одиниці в протилежному випадку, те

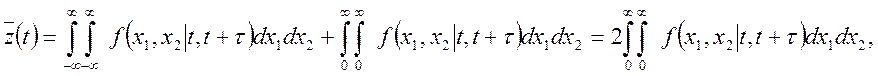
що після виконання інтегрування дає результат, зазначений в умові задачі. (При інтегруванні зручно ввести нові перемінні , , поклавши ).

Задача 2. Знайти одне - і двовимірний закон розподілу і характеристики випадкової функції , заданої своїм канонічним розкладанням

,

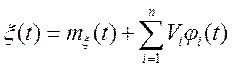де   – взаємно-некореліровані нормально розподілені випадкові величини з характеристиками , .

Рішення. Одномірний закон розподілу  – нормальний з характеристиками ; .

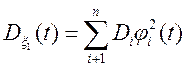Кореляційна функція

.

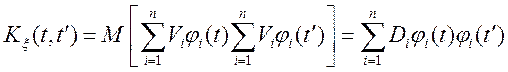Двовимірний закон розподілу  — нормальний з характеристиками , ; ; ; . Випадкова функція  нормальна тому двовимірний закон розподілу є вичерпною характеристикою для будь-якого числа перетинів цієї функції.

Задача 3. Випадкова величина  задана канонічним розкладанням

де і  – некореліровані випадкові величини з математичними чеканнями, рівними нулеві, і з дисперсіями . Визначити, чи є стаціонарної випадкова величина .

Рішення. ; .

Кореляційна функція випадкової функції  задовольняє умові стаціонарності, однак математичне чекання залежить від часу. Випадкова величина  не стационарна, але центрована випадкова величина стационарна.

Задача 4. Похідна стаціонарної випадкової функції. Мається стаціонарна випадкова функція з характеристиками ; , де . Знайти характеристики її похідної  і показати, що вона також стационарна.

Рішення. Тому що  зв'язано з  лінійним однорідним перетворенням, те

;

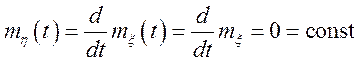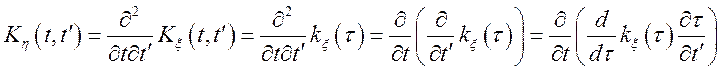
Але 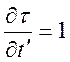 і 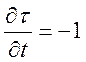, тому .

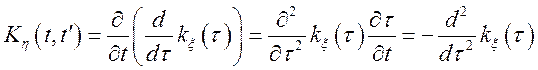Тому що права частина рівності залежить тільки від , те 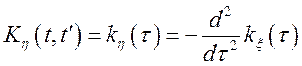 і випадкова функція  стационарна.