МІНІСТЕРСТВО ОСВІТИ Й НАУКИ УКРАЇНИ
СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
Кафедра
«ПРИКЛАДНА МАТЕМАТИКА»
Спеціальність «ПРИКЛАДНА МАТЕМАТИКА»
МЕТОДИЧНА
ДОКУМЕНТАЦІЯ
з курсу «МЕТОДИКА ВИКЛАДАННЯ
МАТЕМАТИКИ
ТА ІНФОРМАТИКИ»
Документ №10
«Контрольні завдання до практичним заняттям»
Луганськ - 2003
Контрольна робота №1
Варіант
1
- Розв’язати нерівність:
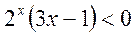 .
.
- Обчислити:
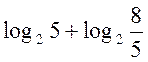 .
.
- Розв’язати систему:
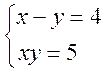 .
.
- Обчислити:
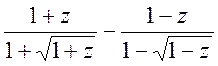 при
при 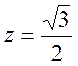 .
.
- Один із суміжних кутів в 8 разів менше іншого. Знайти більший кут.
- Розв’язати рівняння:
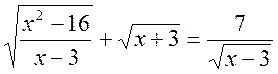 .
.
- Спростити:
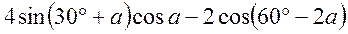 .
.
- Написати рівняння дотичної, проведеної до кривої
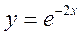 .
.
- Висота циліндра дорівнює
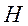 ,
радіус його основи дорівнює
,
радіус його основи дорівнює 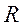 . У циліндр вміщена
піраміда, висота якої співпадає з твірною
. У циліндр вміщена
піраміда, висота якої співпадає з твірною 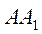 циліндра,
а основою є рівнобедреннний трикутник
циліндра,
а основою є рівнобедреннний трикутник 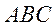
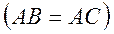 , вписаний в основу циліндра. Знайти
площу бокової поверхні піраміди, якщо
, вписаний в основу циліндра. Знайти
площу бокової поверхні піраміди, якщо 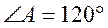 .
.
Варіант
2
- Обчислити значення функції:
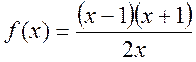 при
при
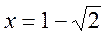 .
.
- При якому значенні
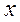 графік функції:
графік функції: 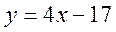 лежить вище осі
лежить вище осі 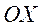 ?
?
- Розв’язати рівняння:
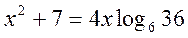 .
.
- Розв’язати систему рівнянь:
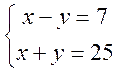 .
.
- При яких значеннях
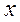 похідна функції
похідна функції 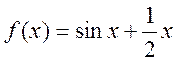 дорівнює нулю?
дорівнює нулю?
- Сума першого й шостого членів арифметичної прогресії дорівнює 6.
Знайти суму перших семи членів цієї прогресії.
- Відомо, що для функції
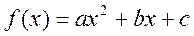 виконуються
нерівності
виконуються
нерівності 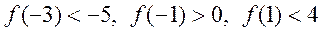 . Визначити знак
. Визначити знак 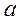 .
.
- Розв’язати рівняння
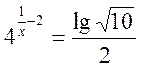 .
.
- Довести, що якщо
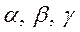 - гуляй
трикутника, те виконується рівність
- гуляй
трикутника, те виконується рівність 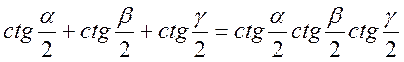 .
.
Варіант
3
- Обчислите значення функції
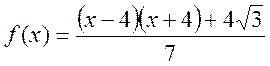 при
при
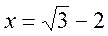 .
.
- При якому значенні
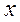 графік функції
графік функції 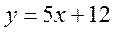 лежить нижче осі
лежить нижче осі 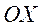 ?
?
- Вирішите систему рівнянь:
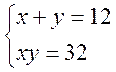 .
.
- При яких значеннях
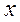 похідна функції
похідна функції 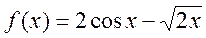 дорівнює нулю?
дорівнює нулю?
- Вирішите рівняння:
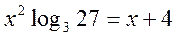 .
.
- Сума третього й дев'ятого членів арифметичної прогресії дорівнює
8. Знайдіть суму перших одинадцяти членів цієї прогресії.
- Відомо, що для функції
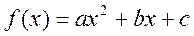 виконані
нерівності
виконані
нерівності 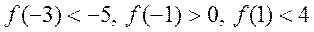 . Визначити знак
. Визначити знак 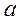 .
.
- Вирішите рівняння:
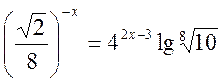 .
.
- Доведіть, що якщо
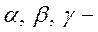 кути трикутника,
то виконується рівність
кути трикутника,
то виконується рівність 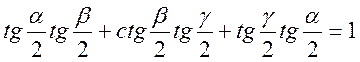 .
.
- Доведіть, що якщо
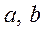 й
й 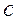 - довжини сторін деякого трикутника,
то при будь-яких значеннях
- довжини сторін деякого трикутника,
то при будь-яких значеннях 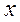 вірна нерівність
вірна нерівність 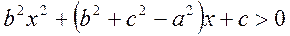 .
.
Варіант
4
- Розв’язати нерівність
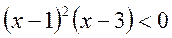 .
.
- Спростити
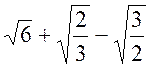 .
.
- Знайти проміжки знакопостійності функції
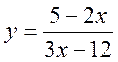 .
.
- Обчислити
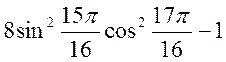 .
.
- Розв’язати рівняння
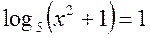 .
.
- Розв’язати систему
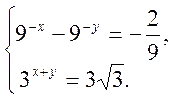
- У трикутнику
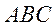
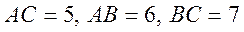 . Бісектриса
. Бісектриса 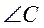 перетинає
сторону
перетинає
сторону 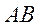 в точці
в точці 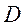 .
Визначити площу трикутника
.
Визначити площу трикутника 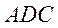 .
.
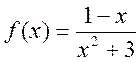 . Знайти
. Знайти 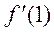 .
.- При якому значенні
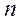 область
визначення функції
область
визначення функції 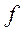 складається з
однієї точки?
складається з
однієї точки?
Варіант
5
- Розв’язати нерівність
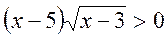 .
.
- Спростити
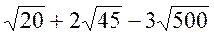 .
.
- Знайти проміжки знакопостійності функції
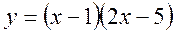 .
.
- Обчислити
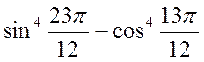 .
.
- Розв’язати рівняння
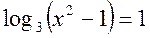 .
.
- Розв’язати систему
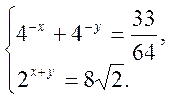
- У трикутник
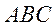
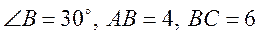 . Бісектриса
. Бісектриса 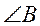 перетинає
перетинає
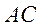 у точці
у точці 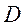 .
Визначити площину трикутника
.
Визначити площину трикутника 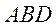 .
.
- При якому значенні
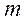 область
визначення функції
область
визначення функції 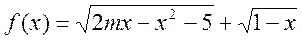 складається з
однієї точки?
складається з
однієї точки?
- Доведіть, що якщо
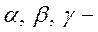 кути трикутника,
то виконується рівність
кути трикутника,
то виконується рівність 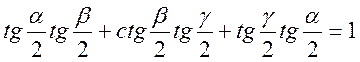 .
.
Варіант 6
1.
Порівняти числа 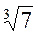 і
і 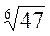 .
.
2.
Знайти 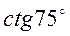 .
.
3.
Розв’язати нерівність 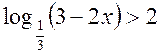 .
.
4.
Розв’язати рівняння 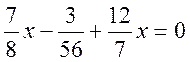 .
.
5.
Різниця двох кутів, одержаних при перетині двох
прямих дорівнює 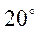 . Знайти більший з цих кутів.
. Знайти більший з цих кутів.
6.
Розв’язати систему рівнянь 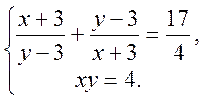
7.
При яких цілих значеннях 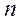 вираз
вираз
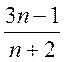 є натуральним числом?
є натуральним числом?
8.
Шматок міді з оловом вагою 12 кг. Містить 45% міді.
Скільки чистого олова необхідно додати до цього шматка, щоб одержаний новий
сплав мав 40% міді.
9. Довести, що 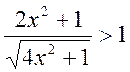 .
.
Варіант
7
- Спростити вираз
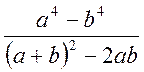 і обчислити при
і обчислити при 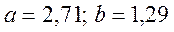 .
.
- Довести
тотожність
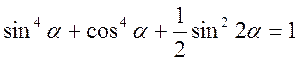 .
.
- Розв’язати
нерівність
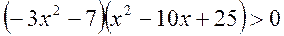 .
.
- Знайти точки
перетину графіка функції
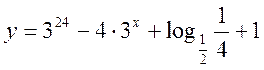 з віссю Ох.
з віссю Ох.
- Знайти
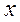 , якщо
, якщо 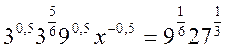 .
.
- Розв’язати рівняння:
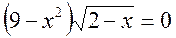 .
.
- Знайти всі
розв’язки рівняння:
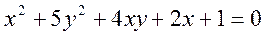 .
.
- Один з катетів
прямокутного трикутника дорівнює 6, медіана проведена до цього катета
дорівнює 5. Знайти гіпотенузу цього трикутника.
- Знайти найбільше
та найменше значення функції
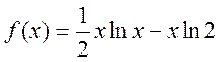 на відрізку
на відрізку 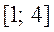 .
.
Варіант 8
1.
Спростити вираз 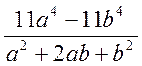 і
обчислити при
і
обчислити при 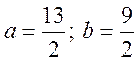 .
.
2.
Довести тотожність 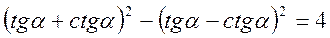 .
.
3.
Розв’язати нерівність 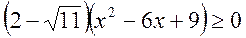 .
.
4.
Знайти точки перетину графіка функції 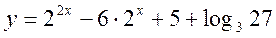 з віссю Ох.
з віссю Ох.
5.
Знайти 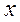 , якщо
, якщо 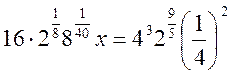 .
.
6.
Розв’язати рівняння: 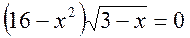 .
.
7.
Знайти всі розв’язки рівняння: 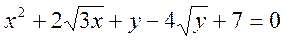 .
.
8.
Один з катетів прямокутного трикутника дорівнює 4.
медіана проведена до цього катета дорівнює 5. Знайти гіпотенузу цього
трикутника.
9.
Знайти найбільше та найменше значення функції 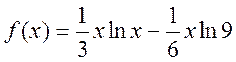 на відрізку
на відрізку 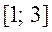 .
.
Варіант 9
1.
Бічні грані правильної трикутної призми – квадрати.
Площа бокової поверхні дорівнює 144. Знайти об’єм многогранника, вершинами
якого є центри всіх граней призми.
2.
Розв’язати систему нерівностей 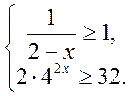
3.
Відомо, що 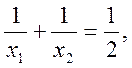 де
де 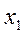 і
і 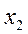 -
корені рівняння
-
корені рівняння 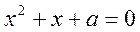 . Знайти
. Знайти 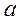 .
.
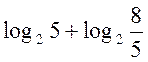 .
.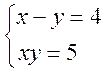 .
.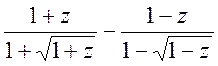 при
при 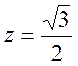 .
.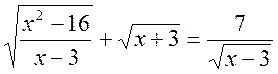 .
.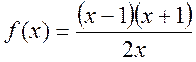 при
при
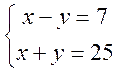 .
.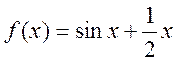 дорівнює нулю?
дорівнює нулю?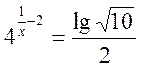 .
.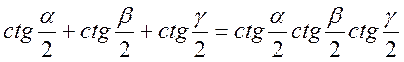 .
.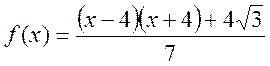 при
при
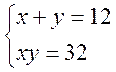 .
.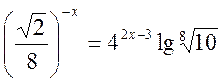 .
.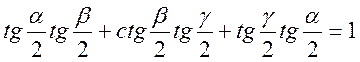 .
.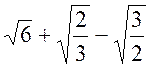 .
.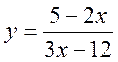 .
.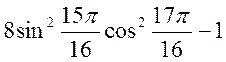 .
.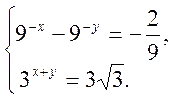
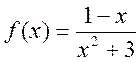 . Знайти
. Знайти 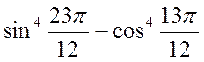 .
.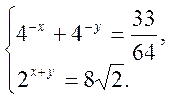
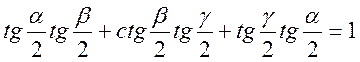 .
.![]() і
і ![]() .
.![]() .
.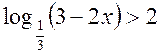 .
.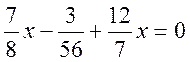 .
.![]() . Знайти більший з цих кутів.
. Знайти більший з цих кутів.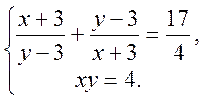
![]() вираз
вираз
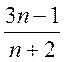 є натуральним числом?
є натуральним числом?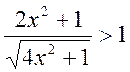 .
.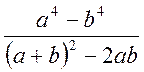 і обчислити при
і обчислити при 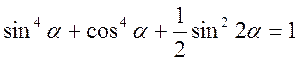 .
.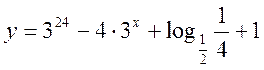 з віссю Ох.
з віссю Ох.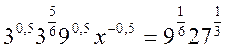 .
.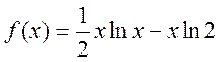 на відрізку
на відрізку 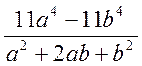 і
обчислити при
і
обчислити при 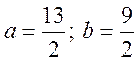 .
.![]() .
.![]() .
.![]() з віссю Ох.
з віссю Ох.![]() , якщо
, якщо 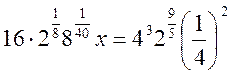 .
.![]() .
.![]() .
.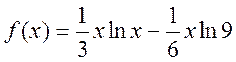 на відрізку
на відрізку ![]() .
.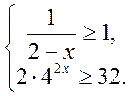
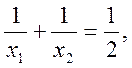 де
де ![]() і
і ![]() -
корені рівняння
-
корені рівняння ![]() . Знайти
. Знайти ![]() .
.