Комплект комплексних контрольних завдань (25 варіантів) з курсу "Методика викладання математики та інформатики"

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

Кафедра «ПРИКЛАДНА МАТЕМАТИКА»

Спеціальність «ПРИКЛАДНА МАТЕМАТИКА»

МЕТОДИЧНА ДОКУМЕНТАЦІЯ

з курсу «МЕТОДИКА ВИКЛАДАННЯ

МАТЕМАТИКИ ТА ІНФОРМАТИКИ»

Документ №11

«Комплект комплексних контрольних завдань»

Луганськ - 2003

Варіант 01

1.         Характеристика основних методів навчання математики: пояснювально – ілюстративний, репродуктивний, проблемний.

2.         Спростити вираз та обчислити його значення при вказаних значеннях букв:

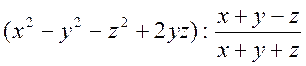 при

3.         Розв’язати рівняння:

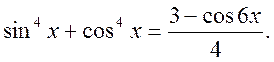
4.         Знайти добуток розв’язків рівняння:

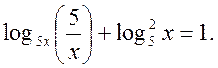
5.         Розв’язати нерівність:

6.  У рівнобедреній трапеції основи дорівнюють 24 і 10, а радіус описаного навколо неї кола дорівнює 13. Знайти висоту трапеції при умові, що центр описаного кола лежить поза трапеції.     

Варіант 02

1.         Математичні поняття. Означення математичних понять, їх види, вимоги до означення понять. Методика формування математичних понять у шкільному курсі математики.

2.         Спростити вираз:

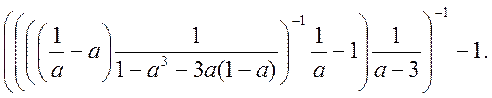
3.         Розв’язати систему рівнянь:

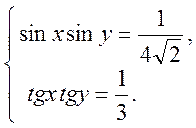
4.         Знайти різницю розв’язків рівняння:

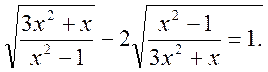
5.         Із точки, що знаходиться на відстані  від площини, проведено дві похилі, які утворюють з площиною , а між собою кут . Знайти відстань між основами похилих.

6.  Знайти найменше та найбільше значення функції  на проміжку .   

Варіант 03

1.         Теореми, їх види, необхідні й достатні умови. Доведення теореми, методи їх доведення в шкільному курсі математики. Методика навчання учнів доведенню математичних тверджень.

2.         Спростити вираз та обчислити його значення при вказаних букв:

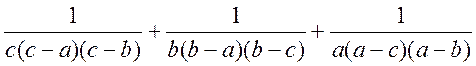
при .

3.         Розв’язати рівняння:

4.         Для яких  значення функці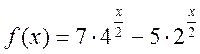ї  і  знаходяться між собою у відношенні більше?

5.         У трикутнику з основою 15см проведено відрізок паралельний основі. Площа одержаної трапеції складає  площі трикутника. Знайти довжину цього відрізка.

6.  Знайти модуль різниці значень функції  в її критичних точках.         

Варіант 04

1.         Задачі в навчанні математиці. Види математичних задач. Характеристика методів в розв’язування задач. Методика навчання учнів розв’язуванню задач.

2.         Розв’язати рівняння:

.

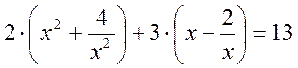3.         Розв’язати систему рівнянь:

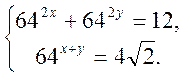
4.         Довести:    .

5.         Для яких  значення функцій  і  знаходяться між собою в відношенні менше.

6.         Знайти площину повної поверхні правильної чотирикутної піраміди, якщо сторона її основи дорівнює , плоский кут при вершині .

Варіант 05

1.         Урок математики. Типи уроків. Вимоги до сучасного уроку математики в школі.

2.         Розв’язати рівняння:

.

3.         Розв’язати нерівність:

.

4.         Обчислити значення , якщо .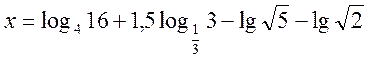

5.         Знайти точки екстремума функції:     .

6.         Осьовий переріз конуса – рівносторонній трикутник. Знайти відношення об’єму конуса до об’єму вписаної в нього кулі.

Варіант 06

1.         Перевірка знань, умінь, навичок учнів з математики та інформатики. Її функції та методика організації.

2.         Знайти проміжки монотонності функції:

.

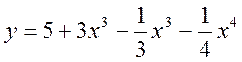3.         Розв’язати рівняння:

.

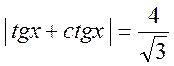4.         Човен проходить 16 км за течією річки на 6 годин швидше, ніж проти течії. При цьому власна швидкість човна на 2 км/год більша від швидкості течії. Визначити власну швидкість човна і швидкість течії річки.

5.         Обчислити:

.

6.         Розв’язати нерівність:

.

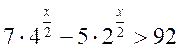Варіант 07

1.         Особливості викладання математики в школах і класах з поглибленим вивченням цього предмету.

2.         Розв’язати нерівність:

.

3.         Розв’язати рівняння:

.

4.         Спростити вираз:

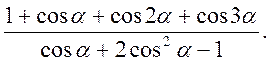
5.         Знайти суму квадратів найбільшого і найменшого значень функції  на відрізку .

6.         У рівнобедреному трикутнику висота відноситься до основи як 3:4, а бокова сторона дорівнює см. Знайти площу трикутника.

Варіант 08

1.         Методика проведення позакласної роботи з математики.

2.         Розв’язати нерівність:

..

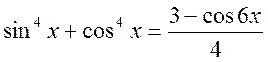3.         Спростити вираз та обчислити його значення при вказаних значеннях букв:

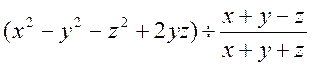 при

4.         Розв’язати нерівність:

.

5.         Знайти добуток розв’язків рівняння:

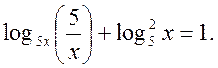
6.         У рівнобедреній трапеції основи дорівнюють 24 і 10, а радіус описаного навколо неї кола дорівнює 13. Знайти висоту трапеції при умові, що центр описаного кола лежить поза трапеції.

Варіант 09