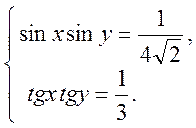
6. Два робітники два рази виконували те саме завдання. Перший раз після спільної триденної роботи другий робітник виконав решту завдання за 15 днів, а другий раз після спільної шестиденної роботи другий робітник виконав решту завдання за 10 днів. За скільки днів кожен робітник зміг би сам виконати все завдання?
Варіант 18
1. Організація самостійної роботи учнів на уроках математики. Домашня робота.
2. Для яких ![]() значення
функцій
значення
функцій ![]() і
і ![]() знаходяться
між собою в відношенні менше.
знаходяться
між собою в відношенні менше.
3. Розв’язати рівняння:
![]()
4. Знайти найменше та найбільше значення функції ![]() на проміжку
на проміжку ![]() .
.
5. Спростити вираз та обчислити його значення при вказаних значеннях букв:
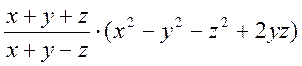 при
при ![]()
6. Із точки, що знаходиться на відстані ![]() від площини, проведено дві похилі, які
утворюють з площиною кут
від площини, проведено дві похилі, які
утворюють з площиною кут ![]() , а між собою кут
, а між собою кут ![]() . Знайти відстань між основами похилих.
. Знайти відстань між основами похилих.
Варіант 19
1. Конспект уроку математики. Загальні методичні вимоги до складання конспекту уроку. Аналіз уроку.
2. Розв’язати рівняння:
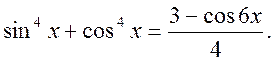
3. Розв’язати нерівність:
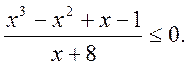
4. Знайти площину повної поверхні правильної
чотирикутної піраміди, якщо сторона її основи дорівнює ![]() ,
плоский кут при вершині
,
плоский кут при вершині ![]() .
.
5. Спростити вираз та обчислити його значення при вказаних букв:
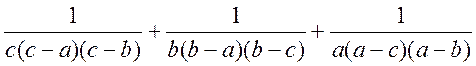
при ![]() .
.
6. Розв’язати систему рівнянь:
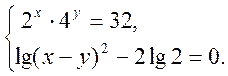
Варіант 20
1. Індивідуалізація і диференціація навчання математики та інформатики. Форми диференційованого навчання математики та інформатики.
2. Знайти нулі функції:
![]() .
.
3. Розв’язати нерівність:
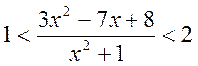 .
.
4. Скільки розв’язків рівняння ![]() знаходиться на відрізку
знаходиться на відрізку 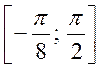 ?
?
5. У трикутнику з основою 15см проведено відрізок
паралельний основі. Площа одержаної трапеції складає ![]() площі
трикутника. Знайти довжину цього відрізка.
площі
трикутника. Знайти довжину цього відрізка.
6. Знайти точки екстремума функції: ![]() .
.
Варіант 21
1. Виховна спрямованість навчання математики та інформатики. Форми та зміст виховної роботи на уроках і в позакласний час.
2. Розв’язати нерівність:
![]() .
.
3. Розв’язати систему рівнянь:
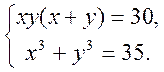
4. Знайти проміжки монотонності функції:
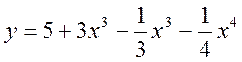 .
.
5. Осьовий переріз конуса – рівносторонній трикутник. Знайти відношення об’єму конуса до об’єму вписаної в нього кулі.
6. Знайти добуток розв’язків рівняння:
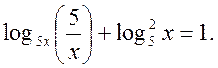
Варіант 22
1. Математичні поняття їх види. Означення математичних понять, їх види, вимоги до означення понять. Методика формування математичних понять у шкільному курсі математики.
2. Розв’язати рівняння:
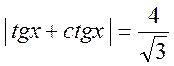 .
.
3. Обчислити:
![]() .
.
4. Розв’язати нерівність:
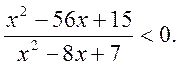
5. Розкласти на множники: ![]()
6. Човен проходить 16 км за течією річки на 6 годин швидше, ніж проти течії. При цьому власна швидкість човна на 2 км/год більша від швидкості течії. Визначити власну швидкість човна і швидкість течії річки.
Варіант 23
1. Конспект уроку математики. Загальні методичні вимоги до складання конспекту уроку. Аналіз уроку.
2. Знайти цілі ![]() , які
задовольняють нерівність:
, які
задовольняють нерівність:
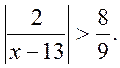 .
.
3. Розв’язати рівняння:
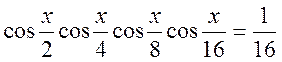 .
.
4. У рівнобедреному трикутнику висота відноситься
до основи як 3:4, а бокова сторона дорівнює ![]() см.
Знайти площу трикутника.
см.
Знайти площу трикутника.
5. Розв’язати систему рівнянь:
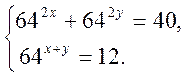
6. Знайти суму квадратів найбільшого і найменшого
значень функції ![]() на відрізку
на відрізку ![]() .
.
Варіант 24
1. Аналіз програм з математики для загальноосвітньої школи. Проблеми досягнення обов’язкових результатів навчання.
2. Спростити вираз:
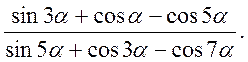
3. Розв’язати рівняння:
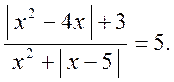
4. Знайти суму квадратів найбільшого і найменшого
значень функції ![]() на відрізку
на відрізку ![]() .
.
5. Розв’язати нерівність:
![]()
6. У рівнобедреній трапеції бічна сторона дорівнює середній лінії, а периметр дорівнює 48. Знайти довжину бічної сторони.
Варіант 25
1. Урок математики. Типи уроків. Вимоги до сучасного уроку математики в школі.
2. Знайти проміжки монотонності функції:
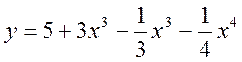 .
.
3. Розв’язати рівняння:
![]() .
.
4. Знайти добуток розв’язків рівняння:
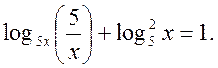
5. Перетворенням лівої частини перевірити, що
![]() .
.
6. Два робітники два рази виконували те саме завдання. Перший раз після спільної триденної роботи другий робітник виконав решту завдання за 15 днів, а другий раз після спільної шестиденної роботи другий робітник виконав решту завдання за 10 днів. За скільки днів кожен робітник зміг би сам виконати все завдання?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.