План:
1. Закон розподілу випадкового процесу.
2. Імовірностні характеристики випадкового процесу.
3. Кореляційна функція і її властивості.
Визначення.Нехай ![]() —
— ![]() значень параметра
значень параметра ![]() .
.
![]() — мірною функцією розподілу випадкового
процесу
— мірною функцією розподілу випадкового
процесу ![]() називається функція
називається функція ![]() перемінних задовольняючій умові
перемінних задовольняючій умові
![]() (2.1)
(2.1)
де ![]() .
.
Визначення. ![]() -мірною щільністю розподілу
випадкового процесу
-мірною щільністю розподілу
випадкового процесу ![]() називається
називається
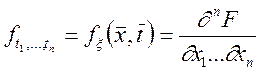 (2.2)
(2.2)
Якщо змішана похідна ![]() —
порядку існує.
—
порядку існує.
Якщо при вивченні випадкового процесу використовується тільки щільність розподілу 1 і 2-го порядків, то говорять, що випадковий процес вивчається в межах кореляційної теорії.
У ряді випадків, як і для випадкової імовірності, для опису випадкового процесу, необов'язкове завдання закону розподілу, а досить визначення деяких характеристик, аналогічно числовим характеристикам випадкової величини. При цьому випадковий процес описується досить повно.
Визначення.Математичним чеканням випадкового
процесу ![]() називають невипадкову величину
називають невипадкову величину ![]() , що при будь-якому фіксованому
, що при будь-якому фіксованому ![]() збігається з математичним чеканням
випадкової величини відповідного перетину випадкового процесу, тобто
збігається з математичним чеканням
випадкової величини відповідного перетину випадкового процесу, тобто
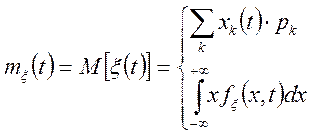 (2.3)
(2.3)
де ![]() —
— ![]() -танучи реалізація випадкового процесу,
-танучи реалізація випадкового процесу,
![]() — імовірність настання
— імовірність настання ![]() -ой реалізації,
-ой реалізації,
![]() — одномірна щільність розподілу.
— одномірна щільність розподілу.
Так само вводиться поняття дисперсії.
Визначення. Дисперсією випадкового процесу ![]() називають невипадкову функцію
називають невипадкову функцію ![]() одному перемінної
одному перемінної ![]() ,
котра при кожнім значенні
,
котра при кожнім значенні ![]() збігається з дисперсією
випадкової величини відповідного перетину випадкового процесу
збігається з дисперсією
випадкової величини відповідного перетину випадкового процесу ![]()
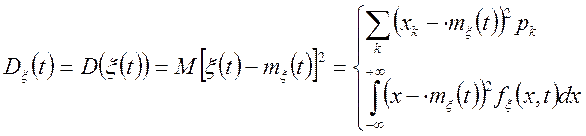 (2.4),
(2.4),
де 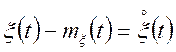 — центрований випадковий процес.
Тоді
— центрований випадковий процес.
Тоді
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
Її розмірність збігається з розмірністю ![]() .
.
Розглянемо два випадкових процеси, заданих безліччю
своїх реалізацій ![]() і
і ![]() .
.
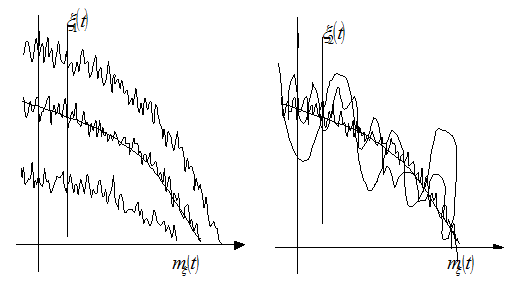
У цих випадкових функцій приблизно однакове математичне чекання і дисперсія, однак, характер їхнього існування різний.
Щоб врахувати ступінь залежності між перетинами
випадкових функцій, що відповідають різним значенням ![]() ,
як і для системи випадкових величин, розглянемо кореляційні моменти значень
випадкового процесу, що відповідають усім можливим значенням параметра
,
як і для системи випадкових величин, розглянемо кореляційні моменти значень
випадкового процесу, що відповідають усім можливим значенням параметра ![]() .
.
Визначення. Кореляційною функцією випадкового процесу ![]() називається невипадкова функція
називається невипадкова функція ![]() двох перемінних
двох перемінних ![]() і
і
![]() , що для будь-якої пари
, що для будь-якої пари ![]() збігається з кореляційним моментом
відповідним двом перетинам випадкового процесу (називається автоковариационной
функцією).
збігається з кореляційним моментом
відповідним двом перетинам випадкового процесу (називається автоковариационной
функцією).
![]()
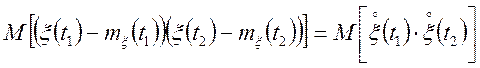 (2.7)
(2.7)
де ![]() — центрований випадковий процес.
У такий спосіб
— центрований випадковий процес.
У такий спосіб
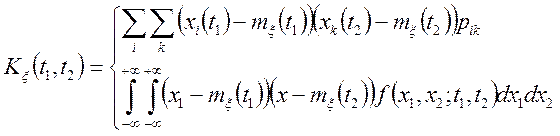 (2.8)
(2.8)
де ![]() — перетину випадкових
процесів у крапках,
— перетину випадкових
процесів у крапках,
![]() ,
,
![]() — двовимірна щільність розподілу випадкового процесу
— двовимірна щільність розподілу випадкового процесу ![]() .
.
Якщо ![]() , то кореляційна функція
перетворюється в дисперсія випадкової величини.
, то кореляційна функція
перетворюється в дисперсія випадкової величини.
Кореляційна функція володіє поруч властивостей:
Властивість 1.
![]() .
(2.9)
.
(2.9)
Доказ.
![]()
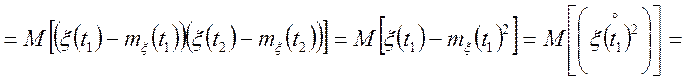
![]() , тобто
, тобто ![]() .
.
Властивість 2 (Симетричність).
![]() . (2.10)
. (2.10)
Доказ.
![]()
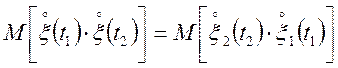 =
=![]() .
.
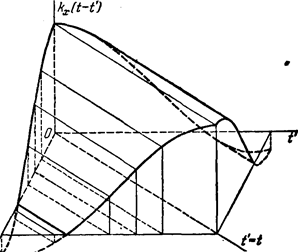
Якщо зобразити кореляційну функцію ![]() у виді поверхні, то ця поверхня буде
симетрична щодо вертикальної площини, що проходить через бісектрису кута.
у виді поверхні, то ця поверхня буде
симетрична щодо вертикальної площини, що проходить через бісектрису кута.
Властивість 3.
![]() . (2.11)
. (2.11)
Доказ.
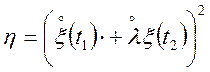 ;
;![]() .
.
![]() ;
; ![]()
![]() (2.12)
(2.12)
Часто замість кореляційної функції ![]() розглядається нормована безрозмірна
кореляційна функція
розглядається нормована безрозмірна
кореляційна функція ![]() — нормована автокорреляционная
функція або просто — автокореляція.
— нормована автокорреляционная
функція або просто — автокореляція.
![]()
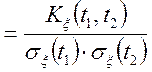 (2.13)
(2.13)
Властивості автокореляції.
Властивість 1.
![]() (2.14)
(2.14)
Доказ.
![]()
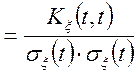
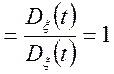 .
.
Властивість 2.
![]()
![]() (2.15)
(2.15)
Властивість 3.
![]() (2.16)
(2.16)
![]() — є аналогом коефіцієнта кореляції, тобто ця функція
несе інформацію про ступінь залежності двох випадкових величин — двох перетинів
випадкового процесу.
— є аналогом коефіцієнта кореляції, тобто ця функція
несе інформацію про ступінь залежності двох випадкових величин — двох перетинів
випадкового процесу.
Приклад. Нехай ![]() випадковий процес.
випадковий процес. ![]() ;
;
![]() ;
; ![]() .
.
Знайдемо
![]() ;
;
![]() ;
;
![]() .
.
Приклад. Нехай ![]() ,
де
,
де ![]() і
і ![]() —
випадкові величини.
—
випадкові величини.
![]() ;
;![]() ;
; 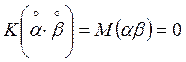 .
.
Знайти
![]() .
.
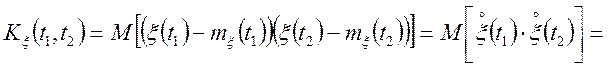
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Приклад.Нехай відома функція щільності розподілу другого порядку
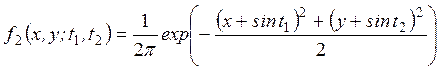 .
.
Знайти ![]()
![]()
![]()
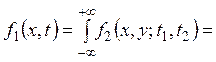
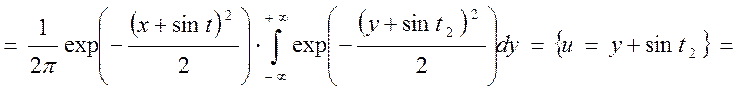
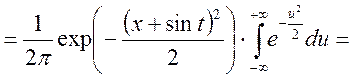 .
.
Отже, перетину ![]() при
при ![]() незалежні.
незалежні.
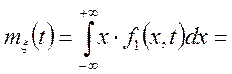
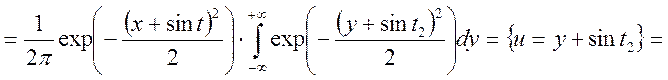
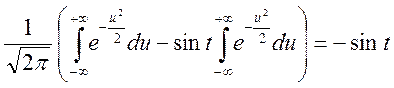
![]()
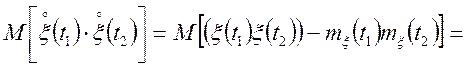
![]()
![]() при
при ![]() , тому
що перетини
, тому
що перетини ![]() незалежні.
незалежні.
Якщо ![]() , то
, то
![]()
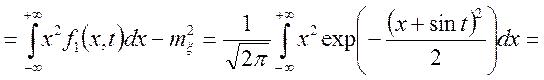
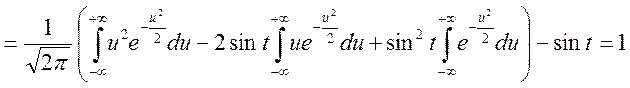 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.