Канонічне розкладання дійсних випадкових функцій. Приклади

Лекція 7

План:

1. Канонічне розкладання дійсних випадкових функцій. Приклади.

1.  Канонічне розкладання дійсних випадкових функцій. Приклади.

При рішенні практичних задач, зв'язаних з роботою динамічної системи, зручно буває випадкову функцию, над якою потрібно зробити ті або інші перетворення, попередньо представити у виді суми так званих елементарних випадкових функцій. Це представлення і складає ідею методу канонічних розкладань, висунуту В.С. Пугачовим.

Визначення. Канонічним розкладанням дійсної випадкової функції  називається її представлення у виді

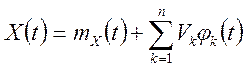,                         (7.1)

де   — невипадкові дійсні, так називані «координатні» функції,   — центровані, попарно некоррелированные випадкові величини з дисперсіями  .

Якщо випадкова величина  представлена канонічним розкладанням (7.1), то її автоковариационная функція записується у виді

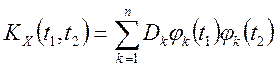.                    (7.2)

Вираження (7.2) називається також канонічним розкладанням автоковариационной функції.

Якщо в представленні випадкової функції

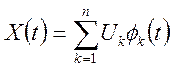                   (7.3)

випадкові величини  коррелированы, те таке представлення не є канонічним розкладанням і тому представлення (7.2) для автоковариационной функції буде несправедливо. Однак, за допомогою лінійного перетворення можна привести вираження (7.3) до канонічного виду.

В основних рисах зазначена задача аналогічна приведенню билинейной або квадратичної форми до канонічного виду, розглянутому в курсі лінійної алгебри.

Приклад. Випадковий процес  заданий вираженням (7.3), де , ,

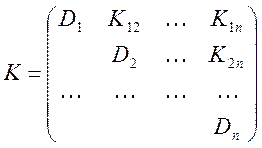 — автоковариационная матриця,

причому 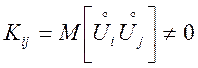, для .

Очевидно, представлення (7.3) не є канонічним розкладанням. Потрібно за допомогою лінійного перетворення привести вираження (7.3) до канонічного виду.

Рішення.

Насамперед центруємо випадкові величини  за допомогою тотожного перетворення:

.

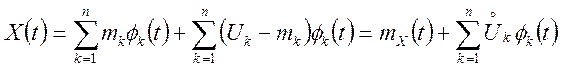Помітимо, що дане вираження може бути записане у виді скалярного добутку:

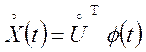,                                     (7.4)

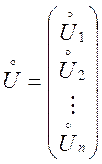де  і , а символ  означає транспонування.

У векторному позначенні автоковариационная матриця записується в такий спосіб:

.

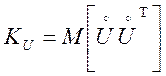Нехай  — новий набір випадкових величин. Виберемо матрицю  таким чином, щоб випадкові компоненти  вектора  були попарно некоррелированы. Маємо

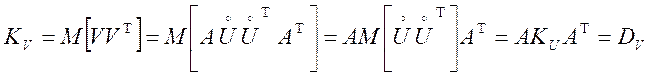, (7.5)

де  — діагональна матриця дисперсій нових компонентів:

.

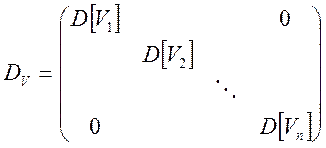З рівності (7.5) укладаємо, матриця  перетворенням «координат» приводить автоковариационную матрицю  до діагонального виду. Оскільки матриця  речовинна і симетрична, то, як доводиться в курсі лінійної алгебри, шукана матриця

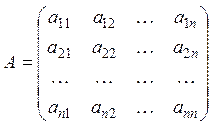
будується в такий спосіб: -я рядок матриці  являє собою -й ортонормированный власний вектор матриці , що відповідає власному значенню . Власні значення   матриці  є коренями рівняння

,

де  — одинична матриця, причому всі  , оскільки матриця  речовинна і симетрична. Якщо зазначена матриця  вже побудована, то

,

причому порядок розташування власних значень  відповідає порядкові запису власних векторів  у матриці . Залишається вибрати новий вектор координатних функцій  з умови незмінності скалярного добутку (7.4). З огляду на, що матриця ортогональна, тобто ( ), і невырожденная, маємо

,

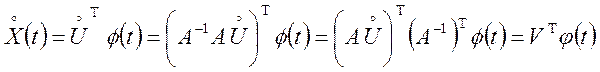де  — перетворений вектор, а

.                    (7.6)

Помітимо, що задача має не єдине рішення. Результат залежить від способу формування ортогональної матриці . Крім того, можна покласти , , якщо вибрати нові координатні функції у виді .

Приклад. Випадкова функція  задана вираженням

, , ,

.

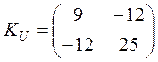Привести дану випадкову функцію до канонічного виду.

Рішення.

Центруємо функцію:

,

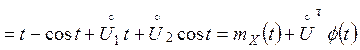де 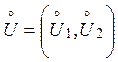, . У даному прикладі зручніше скористатися не ортогональним перетворенням, а методом Лагранжа (аналогічний методові Лагранжа приведення квадратичних форм до канонічного виду). Для цього тотожно перетворимо вираження для ковариационной функції:

.

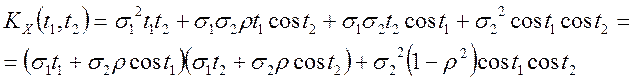Помітимо, що 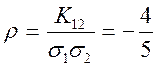. Позначимо

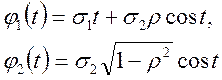                             (7.7)

і покладемо . Матриця перетворення , що вбачається із системи (7.2), має вигляд

.

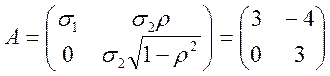Однак, на відміну від випадку розглянутого в прикладі 1, матриця  не ортогональна. Зажадаємо, щоб скалярний добуток  не змінювався при лінійному перетворенні. Тоді аналогічно формулам (6.6) одержимо, що якщо , те . Обчислюючи зворотну матрицю, знаходимо

;

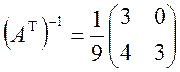таким чином, новий вектор випадкових величин

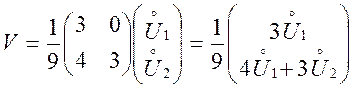                      (7.8)

Перевіримо некоррелированность  і :

.

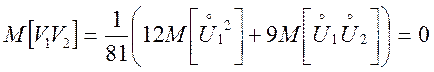Таким чином, одержуємо канонічне розкладання

,

де  і  визначаються рівняннями (7.8), а координатні функції  і  — рівняннями (7.7).

Приклад. Випадковий процес  заданий наступним вираженням: , де 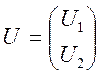 — випадковий вектор з вектором математичних чекань 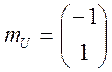 і ковариационной матрицею 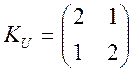; вектор координатних функцій 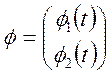. Знайти канонічне розкладання процесу  і записати автоковариационную функцію.

Рішення.

Насамперед, центруємо випадкові величини

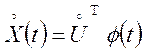,                                      (7.9)

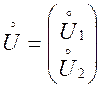де  і 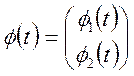, а символ  означає транспонування.

Аналогічно вище розглянутому прикладові 1, знайдемо матрицю . Для цього знайдемо власні вектора матриці

.

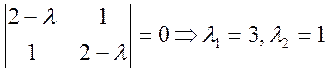Для  одержуємо

.

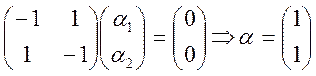Для  одержуємо

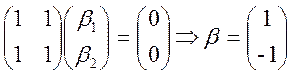
Нормуючи вектори  і , одержуємо відповідні рядки шуканої матриці

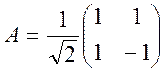
Тоді

, ,

де

, .