






Лекція 11
План:
1. Ергодичний стаціонарний випадковий процес.
1.1. Визначення ергодичного випадкового процесу.
1.2. Визначення ергодичності щодо математичного чекання.
1.3. Достатня умова ергодичності щодо математичного чекання.
1.4. Визначення ергодичності випадкового процесу щодо кореляційної функції.
1.5. Достатня умова ергодичності випадкового процесу щодо кореляційної функції.
2. Нормальні випадкові процеси.
Якщо стаціонарний випадковий процес має властивість, суть якого полягає в тому, що по одній окремій реалізації можна судити про усі властивості випадкового процесу також як по будь-якій кількості реалізацій, то такий процес називається ергодичним.
 (11.1)
(11.1)
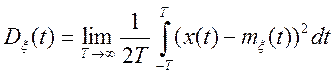
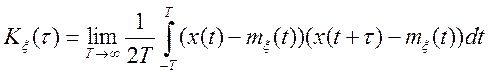 ,
,
де ![]() — деяка реалізація.
— деяка реалізація.
Однак, стаціонарні випадкові процеси можуть мати властивість ергодичності стосовно вероятностным моментів не всіх порядків.
Якщо, наприклад, ![]() можна
визначити як (11.1), то в цьому випадку говорять про ергодичність щодо
математичного чекання.
можна
визначити як (11.1), то в цьому випадку говорять про ергодичність щодо
математичного чекання.
Розглянемо випадкову величину
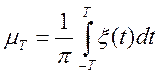 .
.
Визначення. Якщо існує середньоквадратична межа випадкової
величини ![]() для безлічі реалізацій випадкового процесу
для безлічі реалізацій випадкового процесу
![]() при
при ![]() , і не
залежить від вибору реалізації
, і не
залежить від вибору реалізації ![]() , то межа називається ергодичним
щодо математичного чекання, тобто
, то межа називається ергодичним
щодо математичного чекання, тобто
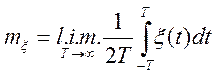
Якщо ж це не виконується, процес не ергодичний.
Теорема. Для того, щоб випадковий процес був ергодичним по
математичному чеканню, тобто щоб ![]() , досить, щоб
кореляційна функція цієї межі задовольняла умові
, досить, щоб
кореляційна функція цієї межі задовольняла умові
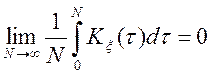 .
(11.2)
.
(11.2)
Наслідок. Достатня умова ергодичності випадкового процесу щодо математичного чекання можна заміняти на більш простої:
![]() .
(11.3)
.
(11.3)
Доказ.
Умова ![]() означає, що
означає, що ![]() існує
існує ![]() таке,
що
таке,
що ![]() , те
, те ![]() . Але
тоді
. Але
тоді
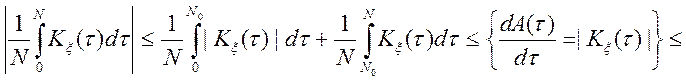
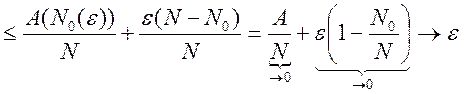
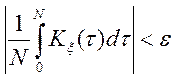 .
.
Таким чином, процес, для якого виконана умова (11.3), ергодичен що до математичного чекання.
Зауваження. Умова ергодичності випадкового процесу щодо математичного чекання (11.2) і (11.3) є достатніми. Разом з тим умова (11.3) може не виконаються, а умова (11.2) — виконується як більш загальне.
Приклад.
![]() .
.
Чи буде процес ергодиен що до математичного чекання?
Рішення.
Перевіримо виконання умови (11.3). Одержимо, що межа не існує.
Перевіримо умову (11.2):
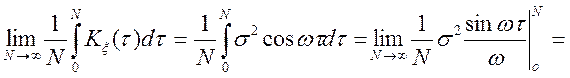
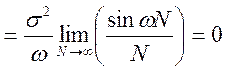 —
—
умова ергодичності виконана, отже процес ергодичен що до математичного чекання.
Для з'ясування умов ергодичності стаціонарного процесу щодо його кореляційної функції, розглянемо його кореляційну функцію.
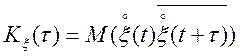 . (11.4)
. (11.4)
Визначення. Процес ![]() називається ергодичнимм
що до кореляційної функції, якщо існує средньоквадратична межа виду
називається ергодичнимм
що до кореляційної функції, якщо існує средньоквадратична межа виду
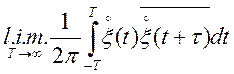
для будь-якої реалізації випадковий процес ![]() і
і 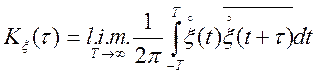 .
.
Теорема. Якщо процес ![]() стаціонарний
у широкому змісті і для процесу
стаціонарний
у широкому змісті і для процесу 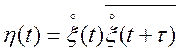 виконується умова
ергодичності по математичному чеканню тобто
виконується умова
ергодичності по математичному чеканню тобто
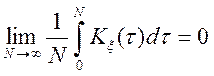 ,
,
те процес ![]() буде ергодичним що до
кореляційної функції, тобто
буде ергодичним що до
кореляційної функції, тобто
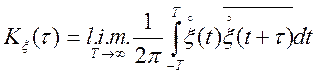 .
.
Визначення. Випадковий процес називається нормальним, якщо ![]()
![]() -мірні щільності імовірностного
процесу нормальні, тобто одномірні щільності:
-мірні щільності імовірностного
процесу нормальні, тобто одномірні щільності:
![]() :
: 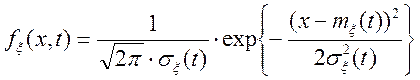 ,
,
![]() :
: 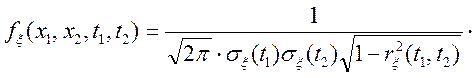
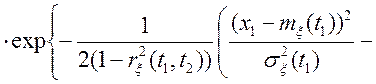
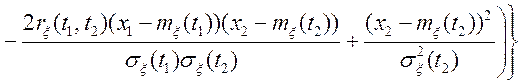 ,
,
![]() :
:
![]()
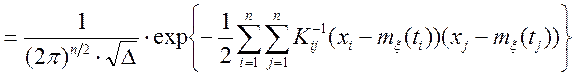 ,
,
де ![]() ,
,
 ,
,
![]() ,
, ![]() .
.
У більш компактній матричній формі:
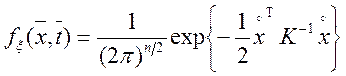 ,
,
де ![]() — вектор-стовпець центрованих
реалізацій випадкового процесу в моменти часу
— вектор-стовпець центрованих
реалізацій випадкового процесу в моменти часу ![]() , а
, а ![]() — матриця, зворотна до автокореляційної,
— матриця, зворотна до автокореляційної, ![]() — визначник матриці кореляцій.
— визначник матриці кореляцій.
З формули для ![]() видно,
що нормальний випадковий процес цілком заданий, якщо відомі його
видно,
що нормальний випадковий процес цілком заданий, якщо відомі його ![]() і
і ![]() .
.
Розглянемо випадковий процес, стаціонарний у широкому змісті.
![]() ,
, ![]() ,
, ![]() ,
,
де ![]() .
.
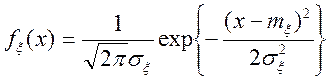 ,
,
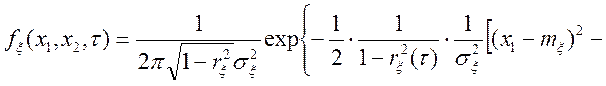
![]() ,
,
де 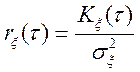 ,
,
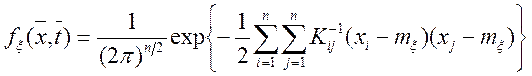 , (11.5)
, (11.5)
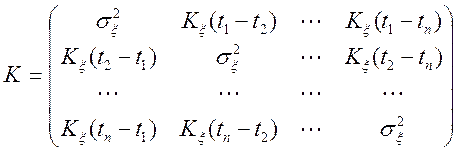 , (11.6)
, (11.6)
де ![]() .
.
Можна показати, що для завдання процесу, стаціонарного
у вузькому і широкому змісті, досить задати ![]() ;
;
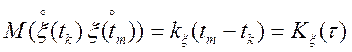 . (11.7)
. (11.7)
Теорема. Якщо нормальний процес стационарен у широкому змісті, то він стационарен і у вузькому змісті.
Доказ.
Якщо він стационарен у широкому змісті, то вірні співвідношення (11.5) і (11.6).
Перевіримо, чи буде виконуватися рівність
![]() .
.
У правій частині вираження для ![]() це
змінить елементи матриці
це
змінить елементи матриці ![]() і визначник
і визначник ![]() , але, згідно (11.7)
, але, згідно (11.7) ![]() . Отже, вираження для
. Отже, вираження для ![]() і
і ![]() не
зміниться, якщо до будь-який тимчасовій перемінного додати те саме постійне
число
не
зміниться, якщо до будь-який тимчасовій перемінного додати те саме постійне
число ![]() . Т.о.
. Т.о. ![]() -мірна
щільність не міняється при зрушенні всіх тимчасових перемінних. Отже,
стаціонарний у широкому змісті процес стационарен і у вузькому змісті.
-мірна
щільність не міняється при зрушенні всіх тимчасових перемінних. Отже,
стаціонарний у широкому змісті процес стационарен і у вузькому змісті.
Теорема. Якщо нормальний випадковий процес стационарен у
широкому змісті, то з умови ![]() випливає, що він
эргодичен як по мат.чеканню, так і по кореляційній функції
випливає, що він
эргодичен як по мат.чеканню, так і по кореляційній функції
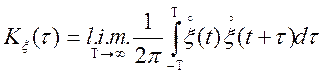 .
.
Теорема. Якщо випадковий процес ![]() нормальний,
то
нормальний,
то 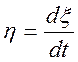 — нормальна функція.
— нормальна функція.
Теорема. Якщо випадковий процес ![]() нормальний,
то
нормальний,
то 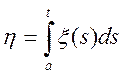 — нормальна функція.
— нормальна функція.
Доказу теорем можуть бути проведені за допомогою характеристичних функцій.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.