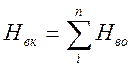Экономика природопользования и природообустройства, менеджмент и маркетинг: Методические указания к проведению практических занятий и для самостоятельной работы студентов, страница 8

,                                               (2.7)

где      n - количество операций, входящих в комплекс.

В нашем случае (по данным таблицы 2) п=3, соответственно Нвк опре­деляется:

,                                        (2.8)

где     - операционные нормы времени соответственно

на валку, обрубку, трелевку. В комплекс также рекомендуется включить опе­рацию - уход за волоком;

комплексную норму выработки, м³/чел. - день:

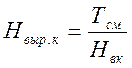,                                                 (2.9)

количество рабочих в бригаде:

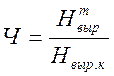,(2.10)

где - сменная выработка ведущего механизма. По условиям рассматриваемого примера ведущим механизмом является трактор.

Таблица 2.3 - Нормы выработки при 8 - часовом рабочем дне по опера­циям, м³/чел. – день

Операция	Наименование   профес­сии	Варианты
		3	4	5	6	7	8	9	10	11	12
Валка деревьев	Вальщик леса Лесоруб	76,9	120,8	99,3	60,6	101,7	81,4	56,7	42,1	25,2	37,3
Обрубка, сбор и укладка сучьев	Обрубщик сучьев	16,5	24.1	20,2	13,0	20,3	16,6	12,4	9,2	6,2	9,2
Трелевка хлыстов тракторами	Тракторист Чокеровщик	33,3	55,9	46	28,1	45,2	37,6	25,8	22	14	11,1

Задание 2.4 Организация выполняет работы по благоустройству терри­тории. В 2002 году объем работ составил 290 тыс.руб., среднесписочная чис­ленность рабочих - 20 человек. Определить плановую численность рабочих па 2003 год, используя метод экстраполяции, если организация планирует увеличить объем работ в 2003 по сравнению с 2002 годом на 15%.

Среднесписочная численность на планируемый период определяется:

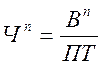,                                             (2.11)

Где ПТ - производительность труда рабочего, тыс.руб.;

В^п  - объем работ в планируемый период.

Задание 2.5 - Определение численности рабочих по благоустройству лесного фонда с использованием математических формул.

Оптимальная численность - это такая численность-, при которой достига­ется максимальная производительность труда (выработка), то есть необходи­мо установить влияние численности на выработку. Но кроме численности на выработку действует множество факторов объективного характера. При построении моделей их влияние должно быть устранено.

В примере, который предлагается для решения в этом разделе, не уда­лось устранить влияния стажа работы. Этот фактор вводится в уравнение, предполагается, что влияние других факторов устранено.

Для упрощения расчетов допускается также, что осуществлены следую­щие действия: установлена независимость факторов, необходимое число на­блюдений, проверены предпосылки, на которых базируется регрессионный анализ, произведен выбор модели - алгебраические полиномы первой степе­ни:

У=В₀+В₁Х₁+В₂Х₂,                                   (2.12)

где      У - комплексная выработка, м³/чел. - день;

X₁ - количество рабочих в бригаде, чел.;

Х₂ - стаж работы, лет.;

В₀, В₁, В₂ - коэффициент модели.

Студент по данным таблицы 2.7 должен выполнить следующие расчеты. Рассчитать коэффициенты уравнения В₀, В₁, В₂:

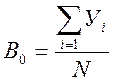,                                    (2.13)

где        N - число наблюдений в рассматриваемом примере N=4, соот­ветственно:

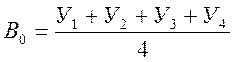,                                (2.14)

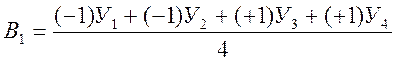,          (2.15)

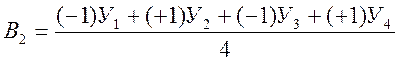,           (2.16)

Приведенные формулы основаны на том, что для получения линейной модели мы установили варьирование факторов на двух уровнях, при этом ис­пользуется кодирование значение факторов: +1 и -1 (например, для первого варианта: четыре человека - это -1, пять человек - это +1).

Таблица 2.4 – Матрица исходных данных для всех вариантов

Номер наблю­дения	Х1	Х2	У
1	-1	-1	У1
2	-1	+1	У2
3	+1	-1	У3
4	+1	+1	У4