Машиностроение \ Проектирование технологического оборудования

Проектирование коробки скоростей (число скоростей = 21) токарно-винторезного станка, страница 6

Профиль зуба определяем при помощи программы «APM Trans», программного модуля «APM Wine Machine». Ход расчета приведен в приложении В.

Повышенные допускаемые напряжения связано с тем, что термообработка зубчатых колес: нормализация и отпуск.

2.6 Уточненный расчет валов

2.6.1 Определение опасного сечения

Целью расчета является проверка диаметров валов с учетом изгибающих и крутящих моментов от всех сил, действующих на вал в различных сечениях.

Проверим на прочность вал II

Крутящий момент на валу ТII = 86 (Н∙м);

Силы в цилиндрических прямозубых зубчатых передачах:

Окружная сила колеса:

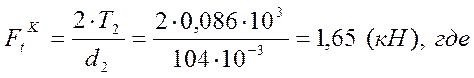 [5]

делительный диаметр колеса (см. табл. 2);

Окружная сила шестерни:

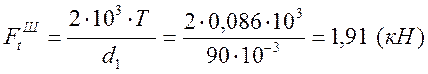 [5]

делительный диаметр шестерни;

Радиальная сила колеса:

 стандартный угол зацепления при ;

Радиальная сила шестерни:

Строим эпюру изгибающих моментов в вертикальной плоскости:

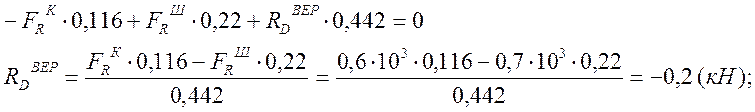
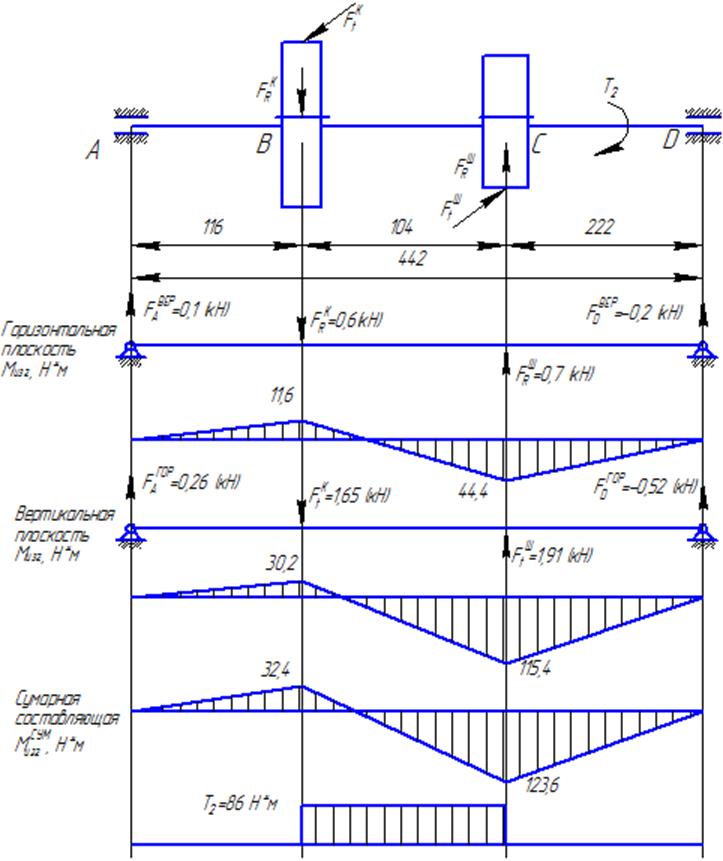
Рисунок 2 - Расчетная схема вала

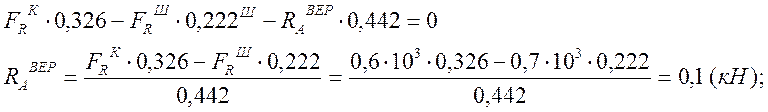
Методом сечений определяем моменты на всех участках:

;

Z – расстояние от реакции.

Строим эпюру изгибающих моментов в горизонтальной плоскости:

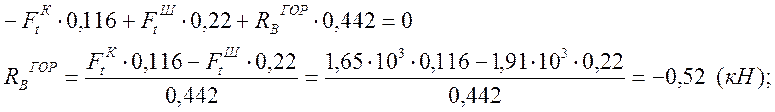
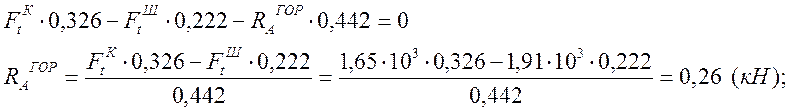
Методом сечений определяем моменты на всех участках:

;

Суммарный изгибающий момент в опасном сечении:

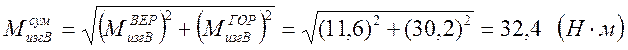 [5]

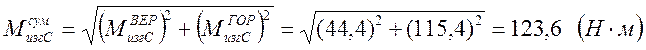
Суммарные реакции в  опорах:

;

 [5]

2.6.2 Расчет на сопротивление усталости

Определим в наиболее опасном  сечении значение коэффициента запаса     усталостной прочности:

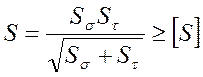, где  [S] = 1,5 - 2,5 [5]

[S] - минимальное допускаемое значение коэффициента  запаса прочности

Выбираем  материал вала:

Ст5:  НВ = 190; s-1 = 220 МПа; t-1 = 130 МПа; yt = 0,06; sв = 520 МПа; tТ = 150 МПа;      sТ = 280 МПа;    [5]

Коэффициент запаса по  нормальным напряжениям:

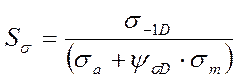, [5] где

  - среднее напряжение цикла;

Так  как нормальные  напряжения изменяются по симметричному  циклу, то          sа = sИ  и sм=0 тогда

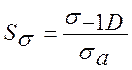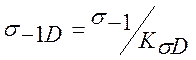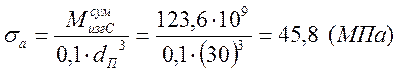, где  ;   [5]

- диаметр вала под подшипник;

s-1D - предел  выносливости вала в рассматриваемом  сечении;

s-1  - предел  выносливости гладких  образцов при симметричном цикле  изгиба;

КsD - коэффициент снижения предела  выносливости;                                      

sа - напряжение в  опасном сечении.

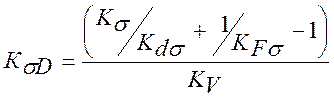  [5]

Кs - эффективный коэффициент концентрации напряжений по табл.10.10; Кs=1,75;

КFs - коэффициент влияния  качества поверхности по табл.10.8.; КFs=1 при Ra≤0,2;                              

KV -  коэффициент  влияния поверхностного  упрочнения по табл.10.9.; КV = 1

Кds - коэффициент влияния  абсолютных размеров поперечного сечения; Кds=0,77;

  ;

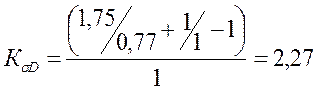Предел  выносливости вала:

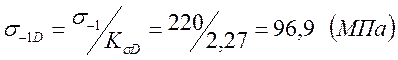 ,[5] тогда

;

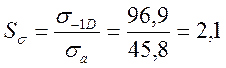Коэффициент запаса по касательным напряжениям:

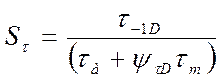   [1]

Так  как касательные изменяются по отнулевому циклу,  то tа=tm=tк/2  [1]

 Амплитуда напряжение цикла в  опасном сечении при кручении:

;

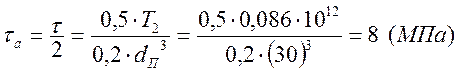Предел  выносливости вала в рассматриваемом  сечении:

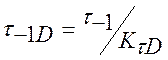, [1] где

t-1 - предел  выносливости  гладких образцов при симметричном цикле  кручения;  

KtD - коэффициент снижения  предела выносливости.

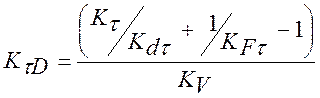, [1] где

Кt - эффективный коэффициент концентрации напряжений по табл.10.10.Кt=1,6;

KFt - коэффициент  влияния качества  поверхности по табл.10.8.; KFt=1 при Ra≤0,2;           

KV -  коэффициент  влияния поверхностного упрочнения по табл.10.9.; КV = 1

Кdt - коэффициент влияния  абсолютных размеров поперечного сечения; Кdt=0,77;

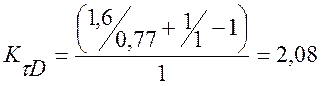,[1] тогда

;

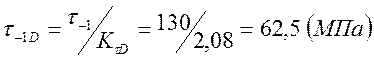Коэффициент чувствительности  к асимметрии цикла:

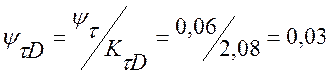, [1] тогда

;

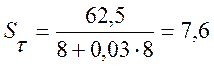Коэффициента запаса усталостной прочности:

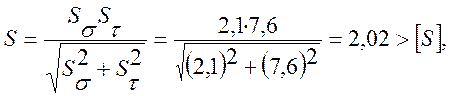 условие выполняется.

Расчет на статическую прочность

при  ; [6]

Напряжение в  опасном сечении при кручении:

;

При расчете учитывают коэффициент перегрузки, берется по табл.24.9.: КП=2,2

При учете максимально действующего кратковременного момента (при пуске);

Напряжение в  опасном сечении при изгибе:

sИ = КП ∙sа =2,2∙45,8=100,8  (МПа) [5];

условие выполняется.

2.6.3 Расчет на жесткость

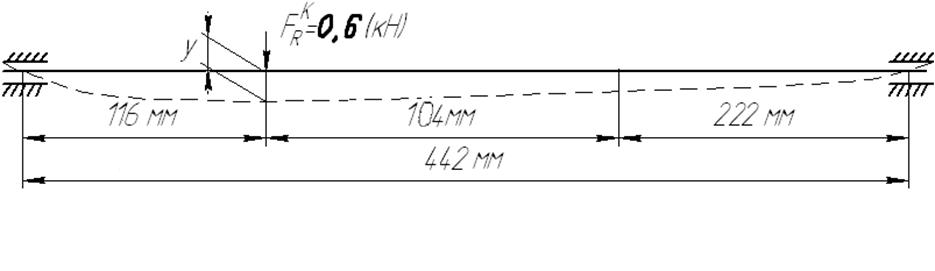
Рисунок 3 - Схема нагружения вала

Угол закручивания вала:

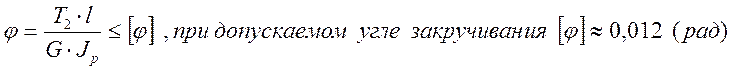, [6] где

- в модуль упругости при сдвиге для стали;

-  момент на валу колеса тихоходной ступени редуктора;

Полярный момент инерции поперечного сечения вала [6]:

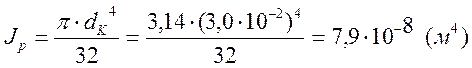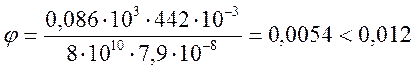,где  диаметр под колесо; условие выполняется.

Прогиб в горизонтальной плоскости от окружной силы на колесе:

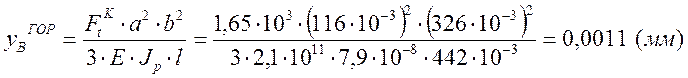,  [3] где

модуль упругости 1-го рода;

Прогиб в горизонтальной плоскости от окружной силы на шестерни:

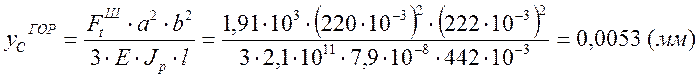 [3]

Скачать файл