Федеральное агентство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Алтайский государственный технический университет
имени И.И. Ползунова»
Бийский технологический институт (филиал)
И.В. Боткин, А.М. Фирсов
ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ УСТАНОВКИ РАЗМЕРА ПО ЛИМБУ СТАНКА
Методические указания к лабораторной работе
Бийск 2006
УДК
ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ УСТАНОВКИ РАЗМЕРА ПО ЛИМБУ СТАНКА
Боткин И.В., ФИРСОВ А.М. Методические указания для выполнения лабораторной работы. Бийск, АлтГТУ. 2006
Алт. гос. тех. ун-т, БТИ, - Бийск
Из-во Алт. гос. техн. ун-та, 2006. – 11 с.
Методические указания предназначены для студентов, изучающих курс «Основы технологии машиностроения»
В указаниях изложены краткие сведения о статистических методах исследования точности обработки, необходимые для уяснения материала при проведении лабораторной работы. Излагается методика проведения лабораторной работы, а также описываются необходимая аппаратура, приспособления и инструмент
Рассмотрены и одобрены на заседании кафедры металлорежущих станков и
инструмента
Протокол № от
Рецензент
© Боткин И.В., 2006
© Фирсов А.М., 2006
©БТИ Алт ГТУ, 2005
СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ
ТОЧНОСТИ ОБРАБОТКИ
При анализе точности технологического процесса приходится рассматривать как систематические, так и случайные погрешности обработки.
Систематической называется такая погрешность, которая в рамках рассматриваемой задачи остается постоянной или же изменяется закономерно.
Случайной называется такая погрешность, которая в рамках рассматриваемой задачи имеет различные значения, причем определить заранее точное ее значение для каждого момента не представляется возможным.
Случайные погрешности вызываются действием на процесс целого ряда независимых, друг от друга случайных факторов. Например, диаметр отверстия при растачивании будет у разных деталей различный, что вызывается неодинаковыми припусками, неодинаковой твердостью обрабатываемого материала, погрешностями измерения и т. п.
Влияние случайных факторов выражается в рассеивании размеров.
Исследование случайных погрешностей основывается на выводах теории вероятности и математической статистики.
При изучении случайных погрешностей изготовления удобно пользоваться кривыми распределения.
Кривые распределения строятся на основании многократных наблюдений одного и того же явления.
Если имеются результаты измерения партии деталей или многократного наблюдения какой-то погрешности изготовления, то построение опытной кривой распределения производится в следующем порядке.
1. Необходимо разбить весь ряд размеров (или показаний) на несколько равных интервалов (удобно брать 5; 7 или 11 интервалов, значение границ интервалов выбирать округленное). Подсчитать количество деталей (или показаний) mi попадающих в каждый интервал размеров.
Если показание попадает на границу интервалов, то необходимо к каждому из смежных интервалов отнести по 1/2 единицы.
2. Отложить по оси абсцисс значения выбранных интервалов и отметить середины интервалов Li (рисунок 1).
3. Отложить на оси ординат в середине каждого интервала частоту mi, т. е. количество деталей (или показаний), попадающих в каждый интервал.
Центр группирования размеров характеризуется средним арифметическим отклонением:
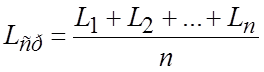
где L1, L2 … – размеры отдельных деталей или результаты отдельных наблюдений;
n – общее число наблюдений или деталей в партии.

Рисунок 1 – Построение кривой распределения.
Для упрощения расчетов практически можно брать средний размер в каждом интервале Li и умножить его на число наблюдений в каждом интервале mi (частоту):
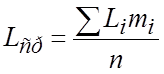
Систематические постоянные погрешности на форму кривой распределения влияния не оказывают и вызывают лишь смещение кривой в направлении оси абсцисс (смещение центра группирования).
Случайные погрешности сказываются как на форме кривой распределения, так и на величине рассеивания размеров.
Величина рассеивания размеров может быть характеризована средним квадратическим отклонением:
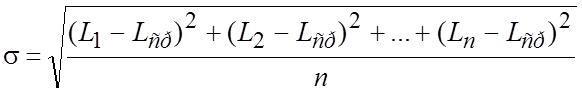 ;
;
или
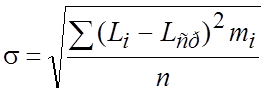
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.