Определение погрешности установки размера по лимбу станка: Методические указания для выполнения лабораторной работы, страница 2

Предельная погрешность, т. е. величина полного рассеивания размеров практически укладывается в пределах ±3s от центра группи­рования (Lср).

В вышеприведенной формуле (L_i — L_ср) отклонение отдельных на­блюдений или размеров деталей от среднеарифметического. Прак­тиче­ски при расчетах можно брать L_i как средний размер в каждом ин­тер­вале и умножать на частоту m_i. Для упрощения вычислений можно вы­читать из L_i не само L_ср (обычно получается число не круг­лое), а его округленное значение L_*ср = L_ср ± a (a — разность между действи­тель­ным значением L_ср и округленным значением) и возвышать его в квад­рат (L_i — L_*ср). В этом случае в числитель надо ввести поправку, так как:

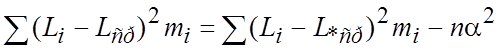
Кривые распределения, полученные на основании данных на­блю­дений, имеют вид ломаных линий (рисунок 1). Вывод каких-либо зако­номерно­стей, имеющих общее значение, на основании рассмотре­ния таких кри­вых представляется затруднительным.

Однако, как показали исследования случайных погрешностей при об­работке деталей, опытные кривые в большинстве случаев прибли­жа­ются к кривым нормального распределения.

Кривая нормального распределения (кривая Гаусса) — это плав­ная теоретическая кривая, которая получается при действии на про­цесс бесконечного числа независимых случайных факторов при бес­конеч­ном числе наблюдений.

Общее уравнение кривой нормального распределения:

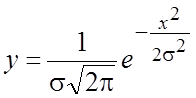
При приведении к обозначениям, принятым при построении прак­тиче­ской кривой распределения, общее уравнение кривой нормаль­ного рас­пределения запишется так:

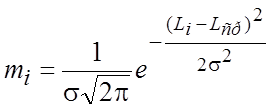
При   построении   необходимо   учитывать   принятые   мас­штабы.

Значит, зная среднеарифметическое отклонение Li и среднее квадра­тическое отклонение s, можно построить кривую нормаль­ного рас­пределения для полученных результатов.

Среднеарифметическое отклонение определит положение кри­вой нор­мального распределения (центр группирования), а среднее квадратическое — высоту и растянутость этой кривой.

Кривая симметрична относительно центра группирования. Гра­фически построение кривой нормального распределения облегчается, если поль­зоваться таблицей ординат, вычисленных при s=1 1 (таблица 1), т. е. для уравнения:

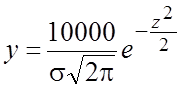
где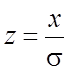        

x=L_i-L_ср - абсцисса, отсчитываемая от центра группирования;

у — ордината   кривой.

Таблица 1

± z	0	0,5	1	1,5	2	2,5	3
±у	3989	3521	2420	1295	540	175	44

Практически для построения ветви кривой нормального распре­деления 2 (рисунок 2) достаточно 5—7 точек, для чего необхо­димо при­нять соот­ветствующее количество значений абсциссы (х).

Первое значение абсциссы, определяющее вершину кривой нор­маль­ного распределения, необходимо принять равным, нулю (х=0).

Последнее значение абсциссы (х) не должно выходить за пре­делы х = 3s. (Можно принять, например, такие значения: х = 0; 0,5s; о; 2s и Зs).

На основании принятых значений х определяют 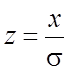 и в таб­лице 1 находят соответствующее значение у.

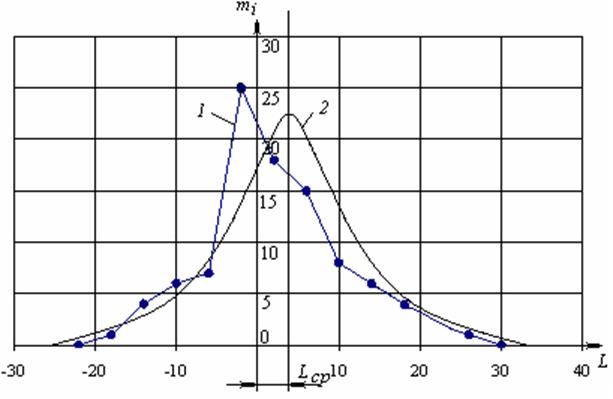
Рисунок 2 – Кривая распределения (/)  и кривая нормального распреде­ле­ния (2).

Для приведения кривой нормального распределения к тому же мас­штабу (частоте), в котором вычерчена практическая кривая рас­пре­де­ления, необходимо ординаты у, найденные по таблице 1 (при s = 1), ум­ножить на масштабный коэффициент. Тогда:

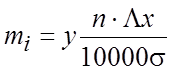
где         m_i  – ордината кривой нормального распределения  (в том же

масштабе, что и у опытной кривой распределения);

у — табличное зна­чение ординаты для s = 1;

Dx— величина интервала (по оси абсцисс), принятая при по­строе­нии опытной кривой распределения (выраженная в тех же единицах, что и s).

Ординаты у при приведении к масштабу делятся на 10 000, так как в таблице 1 их значения умножены на 10 000.

Точки, полученные на графике при построении теоретической кривой нормального распределения, обводятся плавной линией (рису­нок 2).

ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ УСТАНОВКИ РАЗМЕРА ПО ЛИМБУ СТАНКА

При изготовлении деталей на металлорежущих станках часто прихо­дится пользоваться лимбами, дающими возможность отсчи­ты­вать не­обходимые перемещения узлов станка.

При пользовании лимбами (даже при перемещении на целое число де­лений лимба) не представляется возможным точно получить необ­хо­димое перемещение ввиду погрешности  установки.

Погрешность установки размера по лимбу станка является слу­чай­ной погрешностью и зависит от многих переменных факторов, как-то: величины силы трения в направляющих, жесткости цепи пере­меще­ния, износа винтовой пары, зрения рабочего, освещенности рабочего места, ширины штрихов на шкале лимба, неточности шага винта, не­точности нанесения делений на лимбе и др.