Пусть функция f(x) определена в ограниченной замкнутой области D плоскости xOy. Разобьем эту область произвольным образом на n частей. Площадь i-го участка обозначим символом Dsi. На каждом участке произвольно выберем какую-либо точку Pi, и пусть она в какой-либо фиксированной декартовой системе имеет координаты (xi,yi). Составим интегральную сумму для функции f(x,y) по области D, для этого найдем значения функции во всех точках Pi, умножим их на площади соответствующих участков Dsi и просуммируем все полученные результаты:
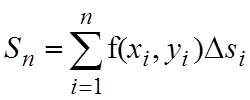 . (1.1)
. (1.1)
Двойным интегралом функции f(x,y) по области D называется предел, к которому стремится последовательность интегральных сумм (1.1) при неограниченном
увеличении числа разбиений n (при этом 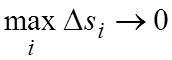 ). Это записывают следующим образом
). Это записывают следующим образом
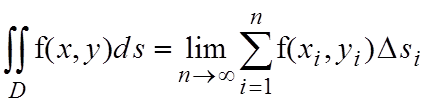 . (1.2)
. (1.2)
Заметим, что если двойной интеграл существует, то он не зависит от способа разбиения области D и от способа выбора точек (xi,yi). Следовательно, область интегрирования можно разбивать при помощи вертикальных и горизонтальных линий. Тогда большинство участков области D будет иметь прямоугольный вид. Поэтому дифференциал площади можно записать в виде ds=dxdy. Следовательно, в декартовой системе координат двойные интегралы можно записывать в виде
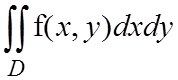 .
(1.3)
.
(1.3)
Если подынтегральная функция f(x,y)º1, то двойной интеграл равен площади области интегрирования:
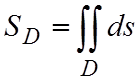 .
(1.4)
.
(1.4)
Свойства двойных интегралов.
10. Интеграл от суммы функций равен сумме интегралов:
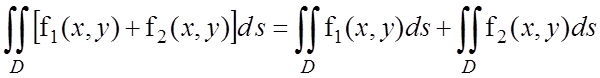 .
.
20. Постоянный множитель можно выносить за знак интеграла:
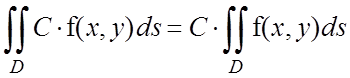 .
.
30. Если область интегрирования D разбить на две части, то двойной интеграл будет равен сумме интегралов по каждой этой части:
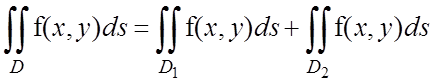 .
.
Повторными интегралами называются интегралы вида
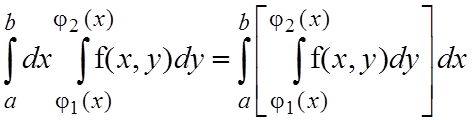 . (1.5)
. (1.5)
В этом выражении сначала вычисляется внутренний интеграл, т.е. производится сначала интегрирование по переменной y (при этом переменная x считается постоянной величиной). В результате интегрирования по y получится некоторая функция по x:
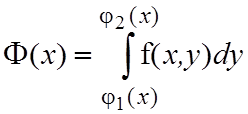 .
.
Затем полученную функцию интегрируют по x:
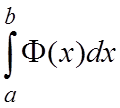 .
.
Пример 1.1. Вычислить интегралы:
а)
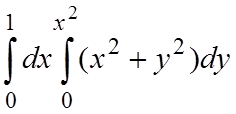 , б)
, б)
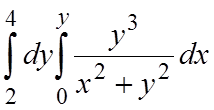 .
.
Решение. а) Произведем интегрирование по y, считая, что переменная x=const. После этого производим интегрирование по x:
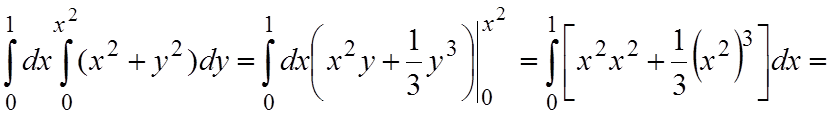
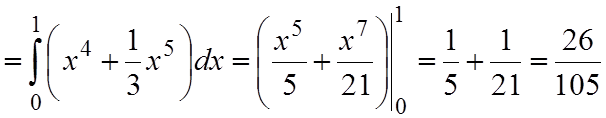 .
.
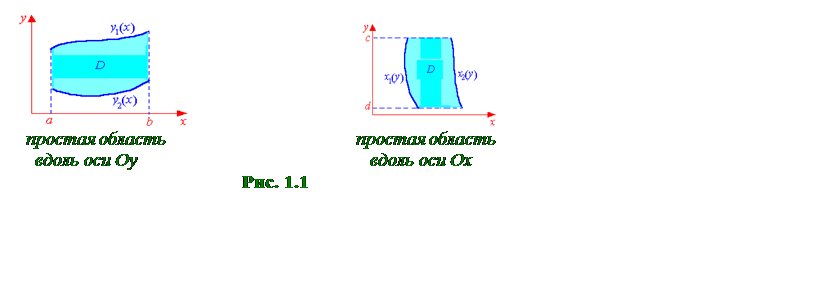
б) Так как во внутреннем интеграле интегрирование производится по переменной x, то y3 можно вынести во внешний интеграл как постоянный множитель. Поскольку y2 во внутреннем интеграле считается постоянной величиной, то этот будет табличным. В результате, получаем
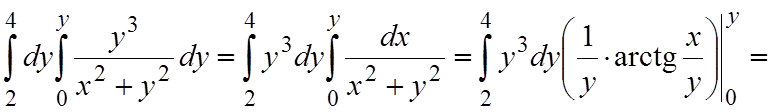
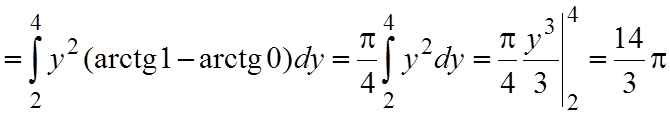 .
.
 |
Любую сложную область можно представить в виде суммы простых областей.
Между двойными и повторными интегралами существует взаимосвязь.
Теорема. Если область интегрирования D – простая в направлении оси Oy (см. рис.1.1а), то двойной интеграл можно записать в виде повторного следующим образом:
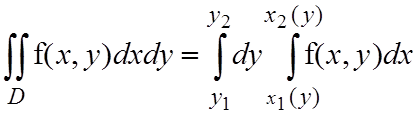 ; (1.6)
; (1.6)
если область интегрирования D – простая в направлении оси Ox (см. рис.1.1б), то двойной интеграл можно записать в виде повторного следующим образом:
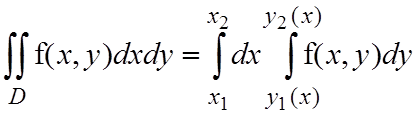 . (1.7)
. (1.7)
Для того, чтобы перейти от двойного интеграла к повторному следует:
1) построить область интегрирования;
2) расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т.е. числами) независимо от того, по какой переменной вычисляется внешний интеграл.
Пример 1.2. Расставить пределы интегрирования в соответствующих повторных интегралах для двойного интеграла
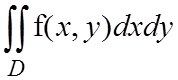 ,
,
если
а) 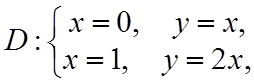 б)
б) 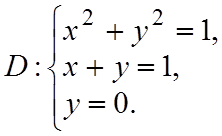
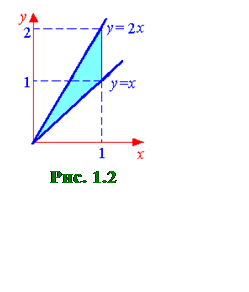 Решение. а) Изобразим
область интегрирования D (см.
рис.1.2). Пусть интегрирование во внешнем интеграле производится по переменной x, а во
внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка
видно, что x изменяется от 0 до 1, при этом значения переменной y будут
изменяться от значений на прямой y=x до значений на прямой y=2x.
Таким образом, получаем
Решение. а) Изобразим
область интегрирования D (см.
рис.1.2). Пусть интегрирование во внешнем интеграле производится по переменной x, а во
внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка
видно, что x изменяется от 0 до 1, при этом значения переменной y будут
изменяться от значений на прямой y=x до значений на прямой y=2x.
Таким образом, получаем
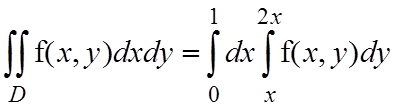 .
.
Пусть теперь интегрирование во внешнем интеграле производится по y, а во внутреннем – по x. В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x=y/2 и x=1. Это означает, что область интегрирования нужно разбить на две части прямой y=1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x=y/2 до прямой x=y. Во второй области y изменяется от 1 до 2, а x – от прямой x=y/2 до прямой x=1. В результате получим
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.