 .
.
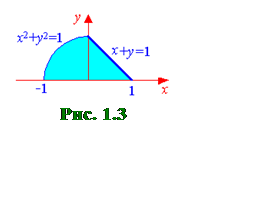 б) Построим область
интегрирования D (см.
рис.1.3). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем
– по y. В
этом случае при изменении x от
–1 до 1 изменения переменной y сверху
будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y=0
до
б) Построим область
интегрирования D (см.
рис.1.3). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем
– по y. В
этом случае при изменении x от
–1 до 1 изменения переменной y сверху
будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y=0
до 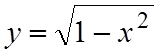 ; на отрезке [0;1] переменная y изменяется от y=0 до y=1–x. Таким
образом,
; на отрезке [0;1] переменная y изменяется от y=0 до y=1–x. Таким
образом,
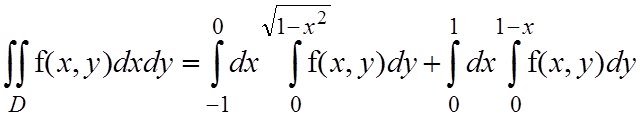 .
.
Пусть
теперь во внешнем интеграле интегрирование производится по y, а во
внутреннем – по x. В
этом случае y будет
изменяться от 0 до 1, а переменная x – от дуги окружности 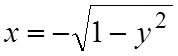 до прямой x=1–y. В результате получим
до прямой x=1–y. В результате получим
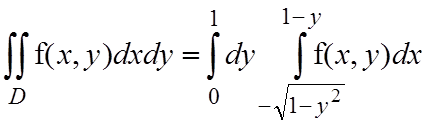 .
.
Данные примеры показывают, как важно правильно выбирать порядок интегрирования.
Пример 1.3. Вычислить двойной интеграл
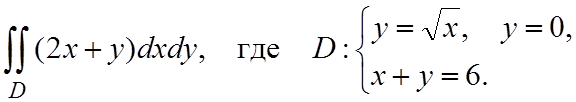
 Решение. Построим область интегрирования (см. рис.1.4).
Расставим пределы в соответствующих повторных интегралах и произведем
вычисления. В результате, получим
Решение. Построим область интегрирования (см. рис.1.4).
Расставим пределы в соответствующих повторных интегралах и произведем
вычисления. В результате, получим
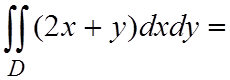
 .
.
Пример 1.4. Вычислить площадь фигуры ограниченной линиями x2=y, x2=4y, y=4.
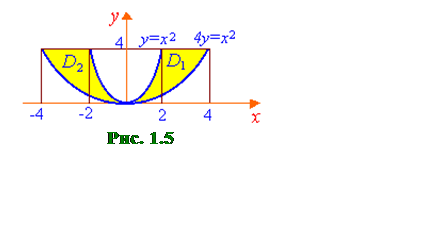 Решение.
Изобразим данную фигуру (рис. 1.5). Видно, что полученная фигура состоит из
двух одинаковых областей: D1 и D2.
следовательно
Решение.
Изобразим данную фигуру (рис. 1.5). Видно, что полученная фигура состоит из
двух одинаковых областей: D1 и D2.
следовательно
 .
.
Интегрирование
во внешнем интеграле будем производить по переменной y (в противном
случае область интегрирования пришлось бы разбивать на две части). Тогда
переменная y будет
изменяться от 0 до 4, а переменная x, соответственно, от параболы ![]() до
параболы
до
параболы ![]() . В результате получаем
. В результате получаем
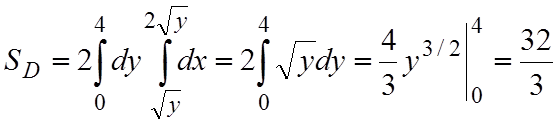 .
.
Наиболее употребительная система координат на плоскости – это полярные координаты. Они связаны с декартовыми координатами x и y равенствами:
![]() (1.8)
(1.8)
где r³0, 0£j<2p.
При переходе от декартовых координат к полярным, двойной интеграл преобразуется следующим образом
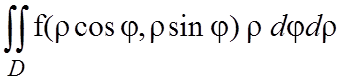 . (1.9)
. (1.9)
Если область интегрирования D является простой в осевом направлении, т.е. любой луч, выходящий из центра координат, пересекает границу области интегрирования не более чем в двух точках, то двойной интеграл можно записать в виде повторного:
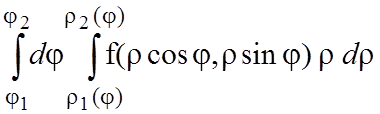 . (1.10)
. (1.10)
Пример 1.5. Вычислить интеграл
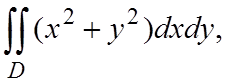 где
где 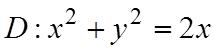 .
.
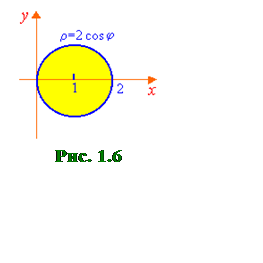 Решение.
Перейдем в полярную систему координат x=rsinj, y=rcosj, x2+y2=r2. Тогда
уравнение границы области D примет
вид r=2cosj. Это есть
уравнение окружности
Решение.
Перейдем в полярную систему координат x=rsinj, y=rcosj, x2+y2=r2. Тогда
уравнение границы области D примет
вид r=2cosj. Это есть
уравнение окружности
(рис. 1.6). Здесь j изменяется от –p/2 до p/2, а r от 0 до окружности r=2cosj. Таким образом, получаем
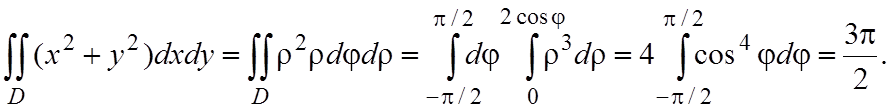
Пример 1.6.
Вычислить площадь фигуры, ограниченной линией  .
.
Решение. Запишем уравнение линии в полярной системе координат
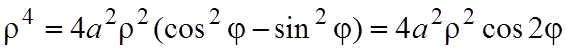 ,
,
 т.е.
т.е.
![]() .
.
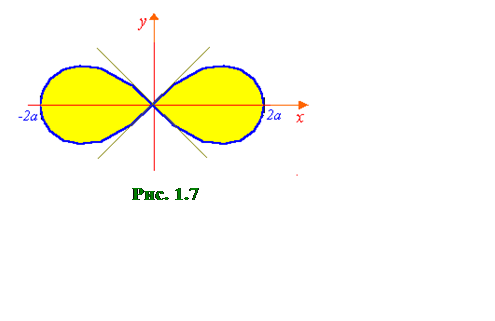
Построим эту линию (рис. 1.7). Поскольку полученная формула симметрична относительно осей Ox и Oy, то достаточно вычислить площадь четвертой части этой фигуры, а затем умножить полученный результат на 4:
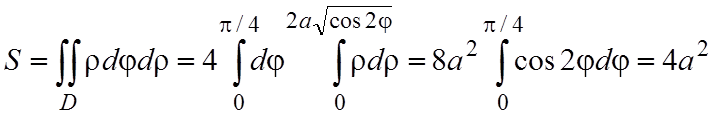 .
.
По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть в некоторой замкнутой ограниченной области T трехмерного пространства задана ограниченная функция трех переменных f(x,y,z). Разобьем эту область на n произвольных частей с объемами Dvi. В каждой частичной области возьмем произвольную точку M(xi,yi,zi) и составим сумму:
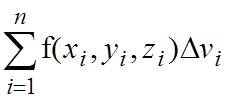 ,
,
которая называется интегральной
суммой для функции f(x,y,z) по области
T. Если интегральная
сумма при n®¥ (при этом диаметры всех областей должны стремится к нулю: 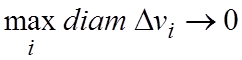 ) имеет предел, то этот предел
называется тройным интегралом:
) имеет предел, то этот предел
называется тройным интегралом:
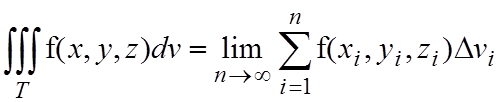 . (2.1)
. (2.1)
Отметим, что тройные интегралы обладают свойствами, аналогичные свойствам двойных интегралов.
Предположим, что область T является простой в направлении оси Oz, т.е. любая прямая, проведенная параллельно оси Oz, пересекает границу области T не более чем в двух точках. Это означает, что область T ограничена снизу поверхностью z=z1(x,y), сверху поверхностью z=z2(x,y) и с боков – цилиндрической поверхностью с образующими, параллельными оси Oz. Тогда тройной интеграл можно записать в виде
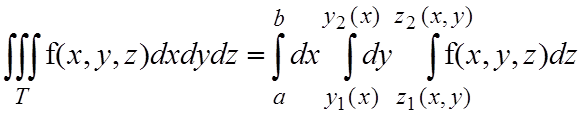 . (2.2)
. (2.2)
Отметим, что здесь внешний интеграл обязательно (!) должен иметь постоянные пределы (т.е. числа), пределы во втором интеграле могут зависеть только от той переменной, которая стоит во внешнем интеграле.
Если в тройном интеграле подынтегральная функция f(x,y,z)º1, то тройной интеграл будет равен объему области интегрирования T, т.е.
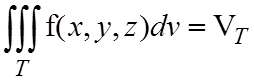 . (2.3)
. (2.3)
При вычислении тройных интегралов следует:
1) сделать чертеж области интегрирования T;
2) изобразить проекцию области T на выбранную координатную плоскость;
3) расставить пределы интегрирования.
Пример 2.1. Вычислить
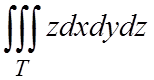 , если
, если 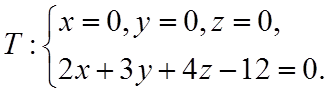
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.