 Пример 3.3. Вычислить работу векторного поля
Пример 3.3. Вычислить работу векторного поля
a = 2x2yi – xy2j
от
начала координат O до точки A(1;1), если движение происходит
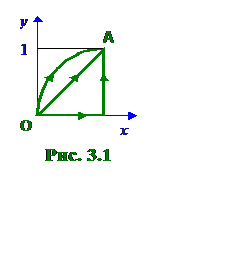
вдоль: а) отрезка прямой [OA]; б) дуги параболы ![]() ;
в) ломаной OBA, где B(1;0) (см. рис. 3.1).
;
в) ломаной OBA, где B(1;0) (см. рис. 3.1).
Решение. а) Уравнение прямой OA имеет вид y=x. Пусть x=t, тогда уравнение прямой в параметрическом виде примет вид:
x=t, y=t,
причем при движении от A до B параметр t будет меняться от 0 до 1. Тогда совершенная работа будет равна
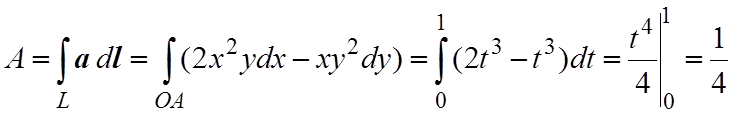 .
.
б) Пусть x=t2, y=t, тогда
x=t2, y=t, 0£t£1.
Далее получаем
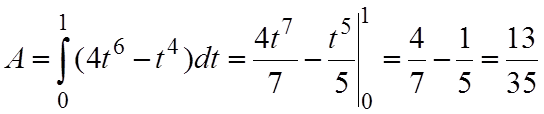 .
.
в) Уравнение прямой (OB) имеет вид y=0 (0£x£1); уравнение прямой (BA) имеет вид x=1 (0£y£1). Тогда
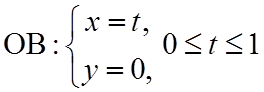 ,
, 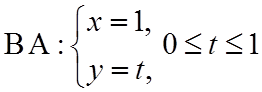 .
.
В результате, получаем,
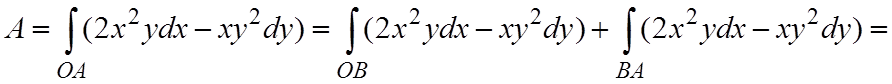
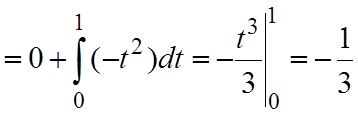 .
.
Замечание. Если в случае двухмерных полей уравнение линии описывается уравнением y=y(x), а переменная x изменяется от a до b, то криволинейный интеграл 2-го будет вычисляться по формуле:
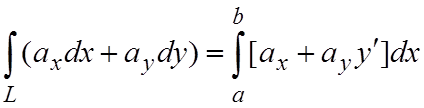 . (3.9)
. (3.9)
Предыдущий пример можно было бы решить и при помощи этой формулы, не вводя параметр t.
Пример 3.4. Вычислить интеграл
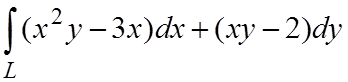 ,
,
где L – дуга параболы y=x2+1 от точки A(0;1) до точки B(2;5).
Решение. Сделаем чертеж (см. рис.3.2). Из уравнения параболы получаем y'=2x. Поскольку на дуге параболы AB переменная x изменяется от 0 до 2, то криволинейный интеграл, в соответствии с формулой (3.9), примет вид
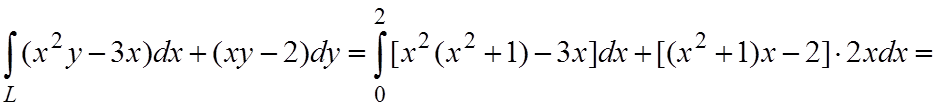
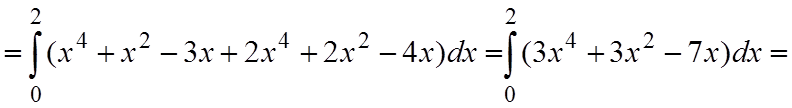
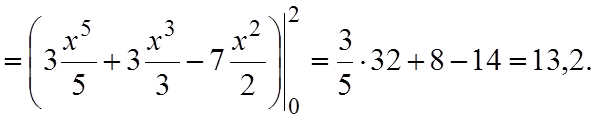
Поверхностный интеграл 1-го рода является обобщением двойного интеграла и вводится аналогичным образом. Рассмотрим некоторую поверхность S, гладкую или кусочно-гладкую, и предположим, что функция f(x,y,z) определена и ограничена на этой поверхности. Разобьем эту поверхность на n произвольных частей. Площадь каждого участка обозначим через Dsi. На каждом участке выберем какую-либо точку с координатами (xi,yi,zi) и вычислим значение функции в каждой такой точке. После этого составим интегральную сумму:
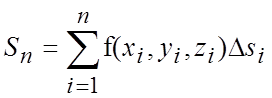 .
.
Если существует предел интегральных сумм при n®¥ (при этом max Dsi®0 ), т.е. такой предел не зависит ни от способа разбиения, ни от выбора средних точек, то такой предел называется поверхностным интегралом первого рода:
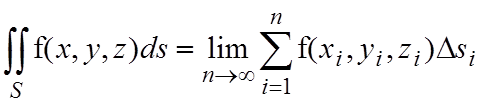 . (4.1)
. (4.1)
Если функция f(x,y,z) непрерывна на поверхности S, то предел (4.1) существует.
Если подынтегральная функция f(x,y,z)º1, то поверхностный интеграл 1-го рода равен площади поверхности S:
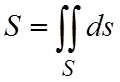 . (4.2)
. (4.2)
Допустим, что введена декартова система координат, и любая прямая, параллельная оси Oz, может пересекать поверхность S лишь в одной точке. Тогда уравнение поверхности S можно записать в виде
z = z(x,y)
и она однозначно проецируется на плоскость xOy. В результате поверхностный интеграл 1-го рода можно выразить через двойной интеграл
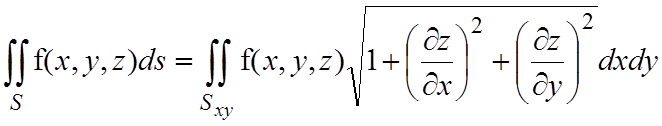 .
(4.3)
.
(4.3)
Пример 4.1. Вычислить интеграл
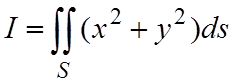 ,
,
где S – часть конической поверхности z2=x2+y2, 0£z£1.
Решение. Имеем
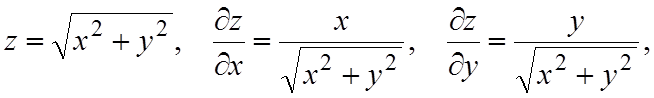
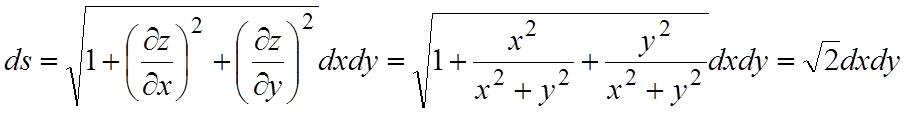 .
.
Тогда искомый интеграл преобразуется в двойной интеграл
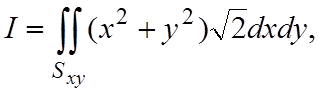
где Sxy – круг x2+y2£1. Поэтому
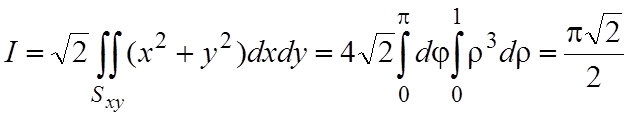 .
.
Пусть в некоторой области задано векторное поле
a = axi + ayj + azk
и какая-либо двухсторонняя поверхность S. Разобьем поверхность каким-либо способом на элементарные площадки DSi. На каждой площадке выберем произвольную точку Pi и составим интегральную сумму:
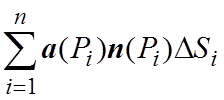 , (4.4)
, (4.4)
где n(Pi) – вектор нормали к заданной поверхности в точке Pi. Если существует предел такой суммы при DSi®0, то этот предел называется поверхностным интегралом 2-го рода (или потоком векторного поля a через поверхность S) и обозначается символом
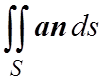 или
или 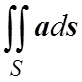 ,
,
где ds=nds.
Поскольку единичный вектор нормали имеет своими координатами направляющиеся косинусы n={cosa, cosb, cosg}. то
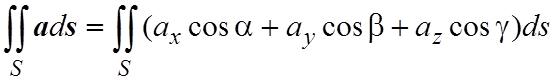 . (4.4)
. (4.4)
Таким образом, вычисление поверхностных интегралов 2-го рода можно свести к вычислению поверхностных интегралов 1-го рода. Однако, что в отличие от поверхностных интегралов 1-го рода интегралы 2-го рода зависят от выбора стороны поверхности. Переход к другой стороне поверхности меняет направление нормали к поверхности, а соответственно и знак интеграла.
Рассмотрим интеграл
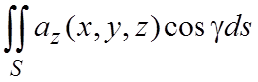 .
.
Пусть уравнение поверхности имеет вид z=j(x,y) и положительной стороной этой поверхности будем считать ту, нормаль которой образует с осью Oz острый угол. Тогда
cosgds = dxdy.
Поэтому рассматриваемый интеграл можно записать в виде
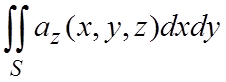 .
.
Заменяя z на j(x,y), придем к двойному интегралу
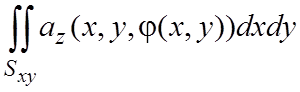 ,
,
где Sxy – проекция поверхности S на плоскость xOy.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.