
Федеральное агентство по образованию
Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)

Лабораторная работа №4
По дисциплине: Физика
Тема: «Исследование затухающих колебаний в колебательном контуре»
Автор: студентка гр. ИЗ-05-2 _________________ / Хорошилова А.Д. /
(подпись) (Ф.И.О.)
Дата: ___________________
ПРОВЕРИЛ: асс. Чернобай В. И.
Санкт-Петербург
2006 год
Цель работы:исследовать зависимость периода колебаний от индуктивности, а также емкости и добротности контура от активного сопротивления.
Краткие теоретические сведения:
Изучаемое явление: возникновение электромагнитных затухающих колебаний в простом колебательном контуре.
Электромагнитные колебания – периодические процессы превращения энергии электрического поля в энергию магнитного поля, и наоборот.
Электрическое поле – вид материи, который создается электрическим зарядом и обнаруживается по действию на электрический заряд.
Магнитное поле – вид материи, которое создается электрическим током и обнаруживается по действию на проводник с током.
Электромагнитное поле – это особая форма материи, осуществляющая взаимодействия между заряженными частицами.
Колебательный контур – цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью C и резистора сопротивлением R.
Конденсатор – система из двух проводников с одинаковым по модулю, но противоположными по знаку зарядами, разделенных диэлектриком.
Емкость конденсатора – физическая величина, которая показывает какой заряд способен накопить конденсатор.
Индуктивность контура – коэффициент пропорциональности, в общем случае зависит от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.
Логарифмический декремент контура – это натуральный логарифм отношения последующих амплитуд заряда конденсатора.
Добротность – величина обратно пропорциональная логарифмическому декременту, следовательно, характеристика резонансных свойств колебательной системы, равная отношению амплитуды установившихся вынужденных колебаний при резонансе к амплитуде вынужденных колебаний вдали от резонанса.
Свободные затухающие колебания – колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.
Электронный осциллограф – прибор, позволяющий регистрировать временный ход электрических процессов с помощью электронно-лучевой трубки, в которой очень узкий пучок электронов используется как карандаш, рисующий изображение.
Теоретически предполагаемый
результат: В
случае затухающих колебаний период равен: 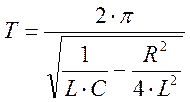 .
Следовательно, графики зависимости периода от индуктивности будут иметь
полиномиальную зависимость, так как индуктивность находится в знаменателе дроби
в степени 1/2, а графики зависимости коэффициента затухания и добротности от
сопротивления будут выглядеть как график натурального логарифма, так как для
вычисления
.
Следовательно, графики зависимости периода от индуктивности будут иметь
полиномиальную зависимость, так как индуктивность находится в знаменателе дроби
в степени 1/2, а графики зависимости коэффициента затухания и добротности от
сопротивления будут выглядеть как график натурального логарифма, так как для
вычисления ![]() и Q мы используем логарифмический декремент контура.
и Q мы используем логарифмический декремент контура.
Схема установки:

С – емкость;
L – индуктивность;
R – активное сопротивление;
K – переключатель, поставленный в положение 1 или 2.
Расчетные формулы:
1.Период затухающих колебаний (с):
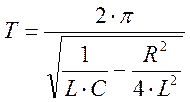
![]()
где:
L – индуктивность (Гн);
C – емкость (Ф);
R – активное сопротивление (Ом).
2.Логарифмический декремент контура:
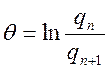
где:
qn и qn+1 – амплитуды заряда конденсатора в момент времени tn и tn+1;
3.Коэффициент затухания (с-1):
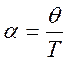
где:
![]() - логарифмический декремент контура;
- логарифмический декремент контура;
T – период (с).
4.Добротность:
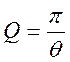
где:
![]() - логарифмический декремент контура.
- логарифмический декремент контура.
Формулы погрешности:
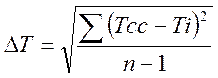
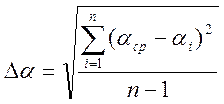
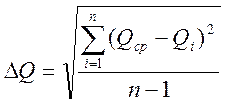
Таблицы для записи результатов измерений
|
№ опыта |
R |
С |
L |
Tэксп. |
Tрасч. |
|
Размерность |
Ом |
Ф |
Гн |
с |
с |
|
1 |
7 |
0,5∙10-6 |
58∙10-3 |
0,84∙10-3 |
1,1∙10-3 |
|
2 |
50∙10-3 |
0,84∙10-3 |
0,99∙10-3 |
||
|
3 |
40∙10-3 |
0,8∙10-3 |
0,89∙10-3 |
||
|
4 |
20∙10-3 |
0,66∙10-3 |
0,63∙10-3 |
||
|
5 |
15∙10-3 |
0,64∙10-3 |
0,54∙10-3 |
||
|
6 |
10∙10-3 |
0,46∙10-3 |
0,44∙10-3 |
2.Исследование зависимости добротности контура и коэффициента затухания от активного сопротивления контура.
|
№ опыта |
С |
L |
R |
Т |
qn |
qn+1 |
|
|
Q |
|
Размерность |
Ф |
Гн |
Ом |
с |
мм |
мм |
с-1 |
||
|
1 |
0,5 |
50 |
10 |
0,84∙10-3 |
5 |
4 |
0,22 |
0,26 |
14,27 |
|
2 |
20 |
0,84∙10-3 |
5 |
3 |
0,51 |
0,61 |
6,16 |
||
|
3 |
30 |
0,8∙10-3 |
4 |
2 |
0,69 |
0,86 |
4,55 |
||
|
4 |
40 |
0,82∙10-3 |
4 |
1,5 |
0,98 |
1,19 |
3,2 |
||
|
5 |
50 |
0,86∙10-3 |
4 |
3 |
0,69 |
0,8 |
4,55 |
||
|
6 |
60 |
0,88∙10-3 |
4 |
2 |
0,69 |
0,78 |
4,55 |
||
|
7 |
70 |
0,88∙10-3 |
3 |
1 |
1,09 |
1,24 |
2,88 |
||
|
8 |
80 |
0,9∙10-3 |
3 |
1 |
1.09 |
1,21 |
2,88 |
Примеры расчёта результатов.
Тэксп1=4,2*0,2*10-3=0,84∙10-3 (с)
Трасч1=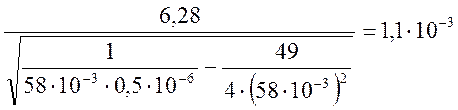 (с)
(с)
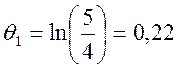
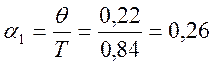
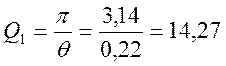
Тср
эксп=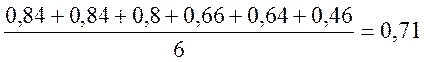 мс
мс
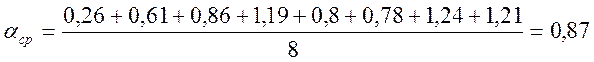
Qср=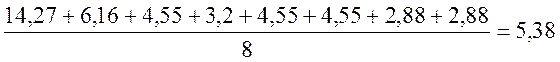
Примеры расчёта погрешностей.
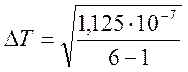 =1,5∙10-4
=1,5∙10-4
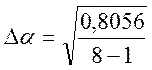 =0,34
=0,34
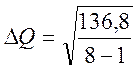 =4,4
=4,4
ΔL=0.5
Класс сопротивления=0,2
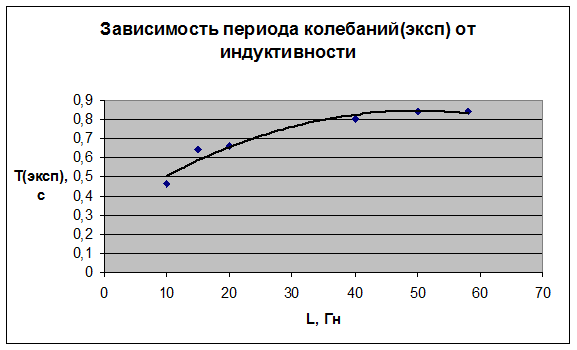
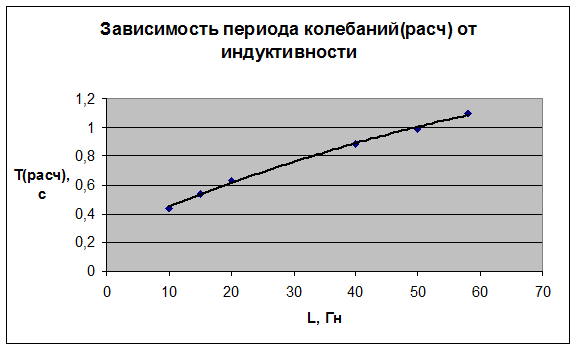
Графики.
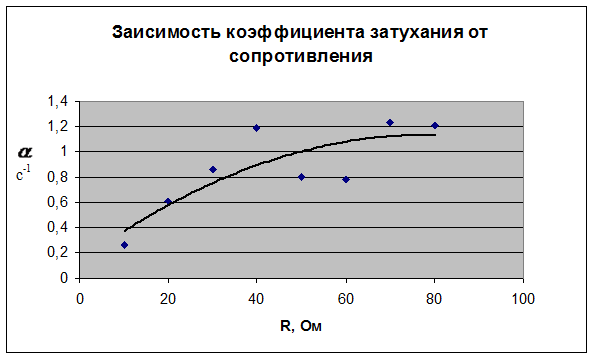
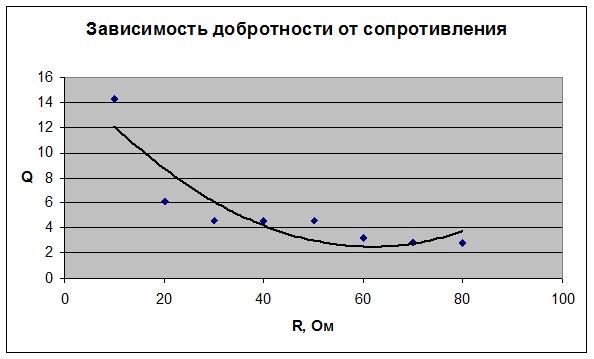
Окончательный результат.
T= 10-3(0,71![]() 0,15) (c)
0,15) (c)
![]() =0,9
=0,9![]() 0,3
0,3
Q=5,4![]() 4,1
4,1
Вывод: Проанализировав полученные результаты, видим, что они почти полностью совпали с предполагаемыми. Графики зависимости Тэксп и Трасч имеют расхождение в связи с тем, что в периоде, измеренном экспериментально, имеет место погрешность измерений прибора
T= 10-3(0,71![]() 0,15). Коэффициент затухания мал
0,15). Коэффициент затухания мал![]() =0,9
=0,9![]() 0,3, следовательно, можно сделать вывод, что потери
энергии в контуре тоже малы. А добротность контура не очень высока,
следовательно, колебательный контур достаточно быстро рассеивает запас энергии
0,3, следовательно, можно сделать вывод, что потери
энергии в контуре тоже малы. А добротность контура не очень высока,
следовательно, колебательный контур достаточно быстро рассеивает запас энергии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.