Кинематическое уравнение движения материальной точки по прямой

Министерство образования

Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра общей и технической физики.

Расчетно-графическая работа №1

	Физика

 

По дисциплине  _____________________________________________________________

___________________________________________________________________________

^{(наименование учебной дисциплины согласно учебному плану)}

	Кинематика движения материальной точки по прямой

 

Автор: студент гр.  НГ-02    ____________________                              /Решитняк Р. В./

                                                               ^{(подпись)                                                        (Ф.И.О.)}

ОЦЕНКА:     _____________

Дата: ___________________

ПРОВЕРИЛ:  руководитель   _________________                                     /Смирнова Н. Н./

                                                                                             ^{(подпись)}

Санкт-Петербург

2003

Вариант № 10.

Задание.

Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид:  x(t) =

Найти:

1)  Среднюю скорость V_ср за интервал времени от t₁ до t₂;  t₁=2.2 c;  t₂=10 с;

2)  Среднюю путевую скорость V_ср.п. за тот же интервал времени;

3)  Среднее ускорение.

Построить графики зависимостей  х(t) и V_x(t).

Краткие теоретические сведения:

Материальная точка – это тело, форма и размеры которого несущественны в данной задаче 

Средней скоростью материальной точки в промежутке времени от t до t +tназывается вектор (V), равный отношению пройденного пути за этот промежуток времени к его продолжительности t.

Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости и равная первой производной от времени t от скорости Vв этой точке.

Координата  - это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве.

Основные расчетные формулы:

            Из кинематического уравнения движения x(t) = 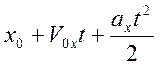 следует, что , это значит, что зависит от времени, тесть движение переменное.

При переменном движении координата материальной точки по оси х имеет вид:

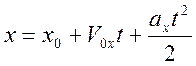, где:

начальное положение точки, проекция вектора начальной скорости. проекция вектора ускорения, t – время.

Скорость:

где:

проекция вектора скорости, V – скорость.

Первая производная координаты по времени есть скорость:

;

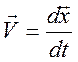Средняя скорость, с которой пройден путь Sза интервал времени от t₁ до t₂:

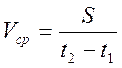; где: S – весь путь.

Средняя путевая скорость за тот же промежуток времени:

;

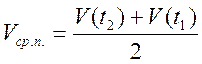При данном условии задачи ускорение не остается постоянным, т.к. зависит от времени, поэтому среднее ускорение будет являться обычным ускорением на участке времени от  до .

Производная скорости по времени есть ускорение:

Расчеты:

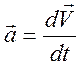
1)          S = x(t₁) – x(t₂) – путь пройденный телом, будет равен разности конечной и начальной его координат.

x(t₁) = =22,14 (м); - координата тела в момент времени .

x(t₂) = 7×10+3×10= 70 (м); - координата тела в момент времени .

S = 22,1452-70= -47,85 (м); - путь пройденный телом.

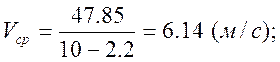 - средняя скорость.

2)         Берем производную:

V(t) =; скорость тела в момент времени t.

 =3-0,09× =2,56 (м/с); - скорость в момент времени .

 =  = -6 (м/с); - скорость в момент времени .

Знак минус показывает, что тело движется в сторону противоположную направлению оси. В расчётную формулу подставляем значения по модулю.

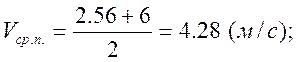
3)   Так как движение у нас переменное, то для проверки возьмем производную:

a =V¢(t) = ()¢ =-0,18t(м/с²)

Знак минус показывает, что движение равнозамедленное.

Графики.

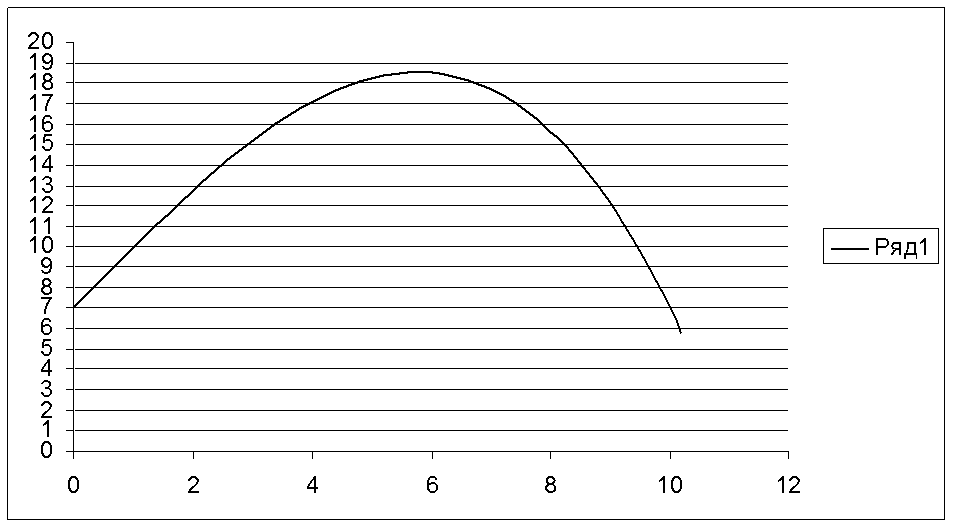
График зависимости x(t):                                        x(t) =7+3

x,м

t,c

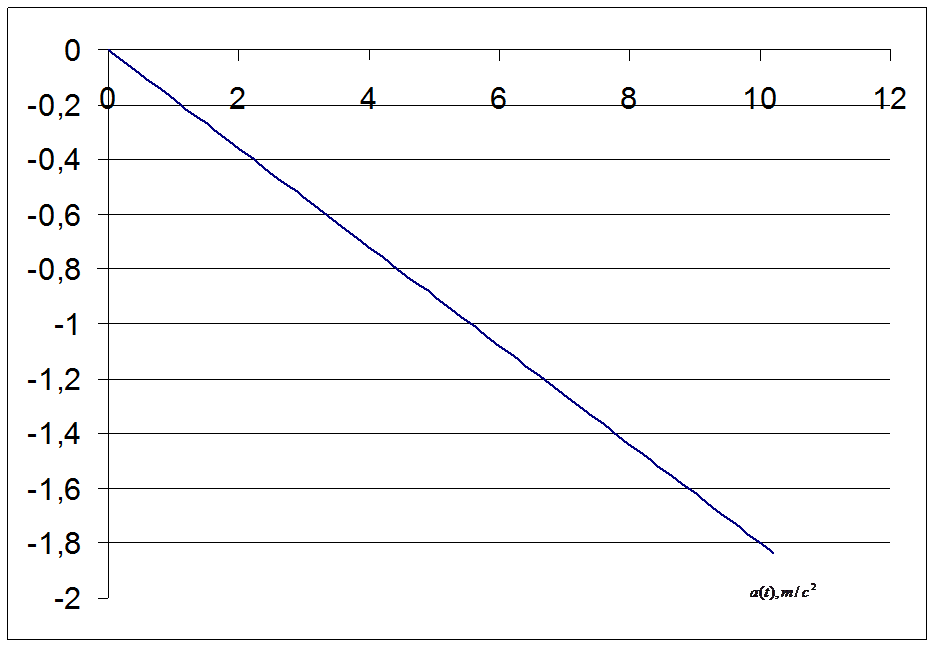
График зависимости a(t):                                      

 

Окончательный ответ:                                                          

1)

2)

3)  a = () м/с².

Вывод.

В результате проделанной работы можно сказать, что при данном кинематическом уравнении движения материальной точки по прямой точка двигалась сначала равнозамедленно, затем остановилась и начала равноускоренное движение в обратную сторону. В расчетах были использованы основные физические формулы движения материальной точки по прямой и дифференцирование.