Определение кинематических и энергетических характеристик при движении заряженной частицы в поле конденсатора

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В.Плеханова

(технический университет)

Кафедра общей и технической физики

Расчетно-графическая работа

Вариант №19

Тема: Определение кинематических и энергетических характеристик при движении заряженной частицы в поле конденсатора

Выполнил: студент гр. НГ-02    /Фаттахов М.М./

Проверил:    доцент                  /Смирнова Н.Н./

                                      (должность)

Дата: _______________

Оценка: _____________

Санкт-Петербург

2003

Формулировка задания

Электрон влетает  в плоский конденсатор под углом a_-=15⁰ к отрицательно заряженной пластине на расстоянии h₀=2 мм от неё.

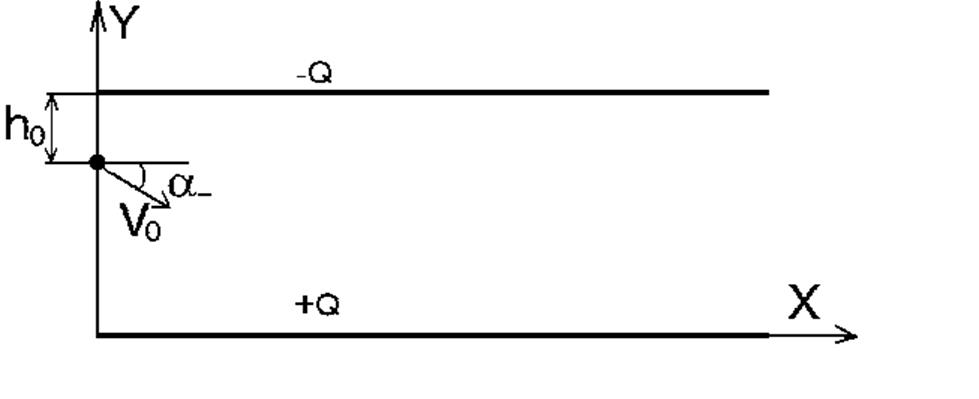Рис 1. Исходные параметры частицы.

Параметры частицы:  

                    q= 1,6∙10^-19 Кл – заряд;

                                m= 9,11∙10^-31  кг – масса;

                                V₀ = 2∙10⁶ м/c – начальная скорость;

         Параметры конденсатора:  

                                Q = 2 мкКл = 2∙10^-6 – заряд конденсатора;

                                l =50 см = 0,5 м – длина пластины (пластина формы квадрата);

                                W= 4 мДж = 4·10^-3Дж – энергия;

Требуется определить:

1.  Начальную энергию частицы Е_о;

2.  Расстояние между пластинами d; емкость конденсатора С;

3.   разность потенциалов между пластинами U;

4.  Рассчитать графические зависимость нормального ускорения частицы от времени полёта в конденсаторе и зависимость скорости её полёта от координаты .

Основные теоретические положения

Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на близком расстоянии d друг от друга и несущих заряды  +Q  и  – Q. Если линейные размеры пластин велики по сравнению с расстоянием d, то электрическое поле между пластинами можно считать эквивалентным полю между двумя бесконечными плоскостями, заряженными разноимённо. Силовые линии поля параллельны друг другу и перпендикулярны пластинам.

Основной характеристикой конденсатора является его емкость – величина, пропорциональная заряду q и обратно пропорциональная напряжению между обкладками:

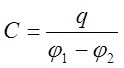                                                                (1)

Разность потенциалов

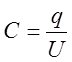                                                                        (2)

 где U– напряжение между обкладками.

Энергией  заряженного  конденсатора  W  называется  полная  энергия  системы  двух  проводников  и  вычисляется  по  формуле:

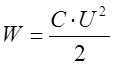                                                                                                                   (3)

Влетая  в  плоский  конденсатор, частица  движется  криволинейно, т.к. на нее действует электрическая сила:

,                                                                    (4)

направленная противоположно линий напряжённости электрического поля  (т.е. противоположно направлению оси Оу) и сила тяжести:

,                                                                    (5)

направленная вертикально вниз (т.е. противоположно направлению оси Оу).

Равнодействующая этих сил направлена вдоль оси Оу и равна:

                                                                 (6)

Проекции равнодействующей силы на оси координат:

                                                                 

                                                                 (7)

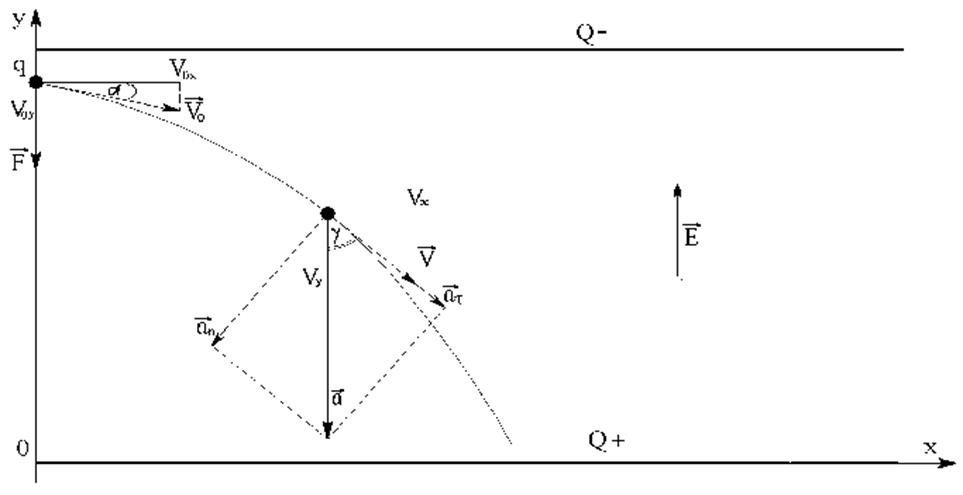
Рис 2.         

При неравномерном движении частицы по криволинейной траектории ускорение можно разложить на два слагаемых. Одно из них коллинеарно скорости и, следовательно, направлено по касатель­ной к траектории. Поэтому его называют тангенциальным (т. е. касательным) ускорением и обозначают а_t . Второе слагаемое является нор­мальным ускорением, которое направлено к центру описываемой электроном кривой; определяется формулой .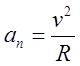

Итак, , первое слагаемое характеризует быстроту изменения модуля скорости, второе слагае­мое – быстроту изменения направления скорости.

Составляющие а_t и а_п перпендикулярны друг к другу. Поэтому квадрат модуля ускорения равен сум­ме квадратов модулей составляющих:Отсюда следует, что:

                                                                (8)

Методика расчета

1.  Определение параметров частицы.

Начальная энергия рассчитывается по следующей формуле:

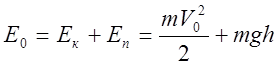                                                             (9)

m – масса  частицы;

V₀ – начальная  скорость;

g – ускорение свободного падения (9,8 м/с²);