Определение числа оборотов цилиндра до достижения им скорости - 2,5 рад/с

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

Кафедра общей и технической физики.

Расчетно-графическая работа

Выполнила: студентка гр. ИЗ-03-1                         МаньшинаТ.В.

Проверила:   доцент                                            Смирнова Н.Н.                  

Дата:

Оценка:

Санкт-Петербург

2004 год

Задача. Сплошной цилиндр массой 0,5кг. вращается без начальной скорости вокруг своей оси. На него действуют пара сил с моментом 21 Дж и моментом сопротивления (κ•ω) Дж. Сколько оборотов сделает цилиндр до того, как его угловая скорость станет равной 2,5 рад/с?

                                    Краткое теоретическое содержание:

• Определение основных величин, процессов, явлений и объектов:

           Цилиндр-тело, ограниченное с концов двумя кругами(основания цилиндра), а с боков - гнутою по кругам плоскостью(боковая поверхность).

При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Угловая скорость – векторная величина, модуль которой определяется формулой:

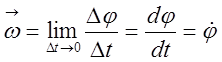, характеризует быстроту вращения, ориентацию оси вращения в пространстве и направление вращения. Единица угловой скорости [рад/с].

Момент инерции тела – величина , равная сумме произведений элементарных масс на квадрат их расстояний от некоторой оси.

Момент инерции для цилиндра равен 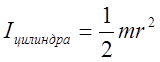. Единица измерения момента инерции [кг•м²].

Пара сил – две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой.

Моментом силы называется векторная величина, модуль которой равен произведению силы на плечо. , .

Плечо – кратчайшее расстояние от оси вращения до линии действия силы.

Если на тело действуют два момента сил, вызывающих вращение в противоположных направлениях, то один из них условно считают положительным, а второй отрицательным.

Число оборотов равно: 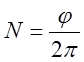, где N – число оборотов, φ – угол поворота, рад.

•  Законы и соотношения, используемые при решении:

Второй закон Ньютона:, подставляя в закон аналогичные характеристики для вращательного движения получим:

второй закон Ньютона

 для вращательного движения:

,

где М – момент силы, Н•м;

I – момент инерции, кг•м²;

ε – угловое ускорение, рад/с².

Момент инерции для цилиндра равен 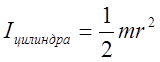, где

          масса цилиндра, кг;

 радиус цилиндра, м

 Единица измерения момента инерции [кг•м²].

Угловая скорость равна: 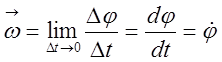   , где

           угол поворота тела, рад;

время движения, с

Единица измерения угловой скорости [рад/c].

    Угловое ускорение равно: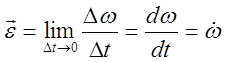 , где

     угловая скорость, рад/c;

время движения, с

Единица измерения углового ускорения [рад/c²].

Число оборотов, совершаемых цилиндром, равно:

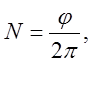 где             угол поворота тела, рад;

Решение:

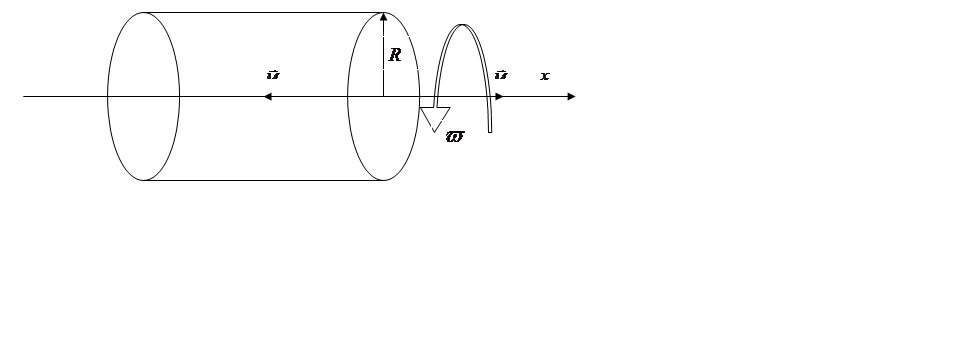
Обозначим момент сопротивления (силы трения) – М₂, момент силы вращения цилиндра – М₁.

Согласно второму закону Ньютона для вращательного движения (), следует .

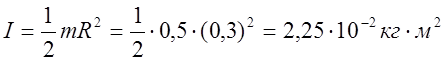 т.к. (по условию) следовательно .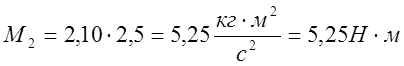

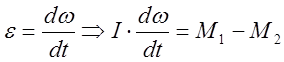
проинтегрируем это выражение:

, но с=0, т.к. по условию задачи тело движется из состояния покоя t = 0 и ω = 0.

 .

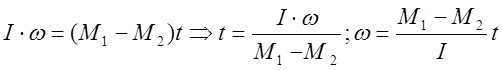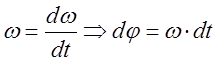
проинтегрируем:

(но с = 0)

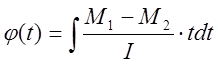
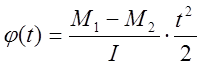
т.к. 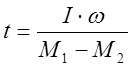, то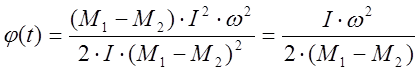  

.

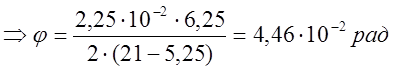
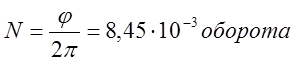Вывод: Используя вышеперечисленные законы и соотношения, можно вычислить число оборотов цилиндра до достижения им скорости--2,5 рад/с.  Таким образом, цилиндр сделает 8,45•10^-3 оборота, до того, как его угловая скорость станет равной 2,5 рад/с. Т.е. цилиндр не успеет сделать даже полный оборот, когда его скорость станет уже 2,5 рад/с, следовательно, приложенная к нему сила достаточно велика по значению.