Определение кинематических и энергетических характеристик при движении заряженной частицы в поле конденсатора, страница 2

h – высота на которой находится частица при попадании в конденсатор                                                                                                                      (h=d–h₀).

2.  Определение параметров конденсатора.

Емкость конденсатора из (3):

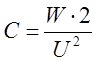                                                                           (10)

Величина емкости определяется также геометрией конденсатора и  диэлектрическими свойствами среды, заполняющими пространство между обкладками.

Из формулы для ёмкости плоского конденсатора найдём расстояние между обкладками:

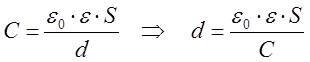                                              (11)

С – электроемкость  плоского  конденсатора;

e₀ – диэлектрическая проницаемость вакуума, e₀=Ф/м;

e – относительная диэлектрическая проницаемость вещества заполняющего зазор, e=1 (воздух);

S – площадь  пластины,  S=l² ;

l – длина  пластины.

Величина напряжения из (2):

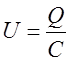                                                               (12)

Подставив (12) в (10) находим электроемкость:

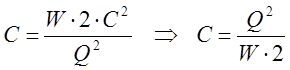                                           (13)

Оценим численные значения сил, действующих на частицу:

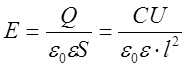                                                              (14)

Подставим (14) в (4):

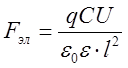                                                                               (15)

Выполнение расчетов

1. 

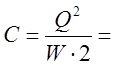
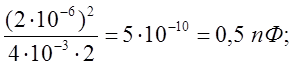
2. 

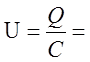
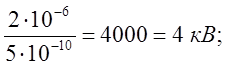
3. 

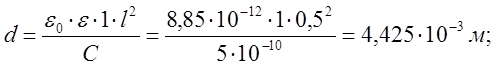
4.  ==

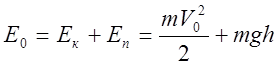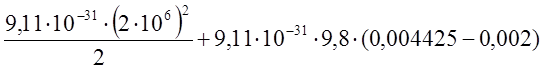=1,822∙10^-18 Дж;

Вычислим по формуле (15):

                                   

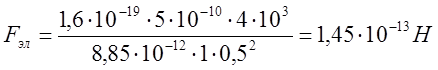
Вычислим по формуле (5):

                                   

Получили:

Поэтому в дальнейших расчётах силой тяжести можно пренебречь, и считать, что заряженная частица в конденсаторе движется только под действием электрических сил, то есть:

Определение графических зависимостей

Определение графической зависимости V(x):

1.  Вдоль оси Ох заряд движется равномерно (=0):

                                                            (16)

2.  Вдоль оси Oy заряд движется равноускоренно под действием постоянной электрической силы:

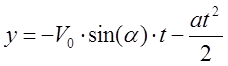
3.  Скорость частицы

- по оси Ох: 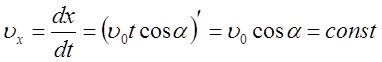                                                   (17)

- по оси Оу: 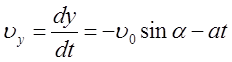                                                                            (18)

4.  Скорость частицы

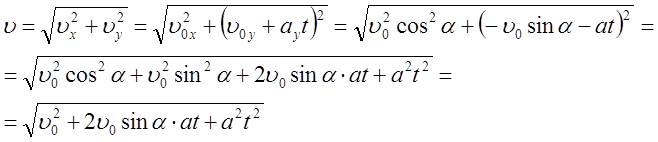                           (19)       

5.  Из (16) находим:

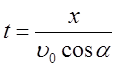                                                            (20)

6.  Подставим (20) в (19):

                       

Получили зависимость:

                                                                    

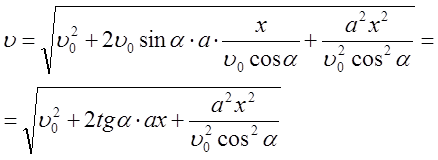
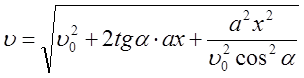
7.  Электрическая сила: F=qE, где Е – напряженность электрического поля в конденсаторе, Е=U/d. Используя второй закон Ньютона найдем ускорение частицы:

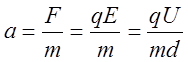                                                        (21)

8.  Следовательно:

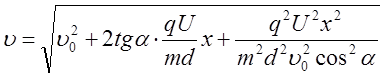;         V = 8·10¹⁰x + 991465

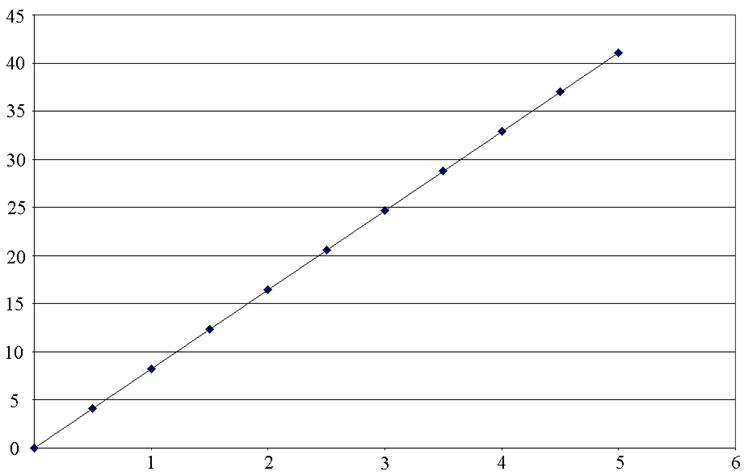
График зависимости V(x):

*10⁸ V, м/с  

x *10-2 м	V *108 м/с
0	0,02
0,5	4,11
1,0	8,22
1,5	12,3
2,0	16,4
2,5	20,6
3,0	24,7
3,5	28,8
4,0	32,9
4,5	37,0
5,0	41,1

*10^-2 x, м   

Определение графической зависимости а_n(t):

1.  Полное ускорение , где  – являются проекциями  на направление соответственно нормали и касательной проведенной в точке (см. рис. 2). Модуль нормального ускорения:

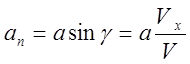, где                                                    (22)

     V – модуль скорости, V_x – проекция вектора скорости на Ох

                                                            (23)

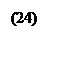
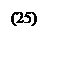подставив (21) в (18):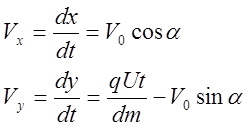        

   Решив совместно 22–25 равенства, получим зависимость нормального ускорения от времени:

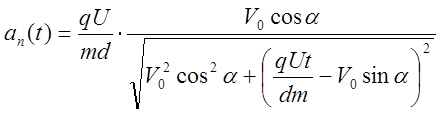;          a_n = 2·10⁶·t^-1: 

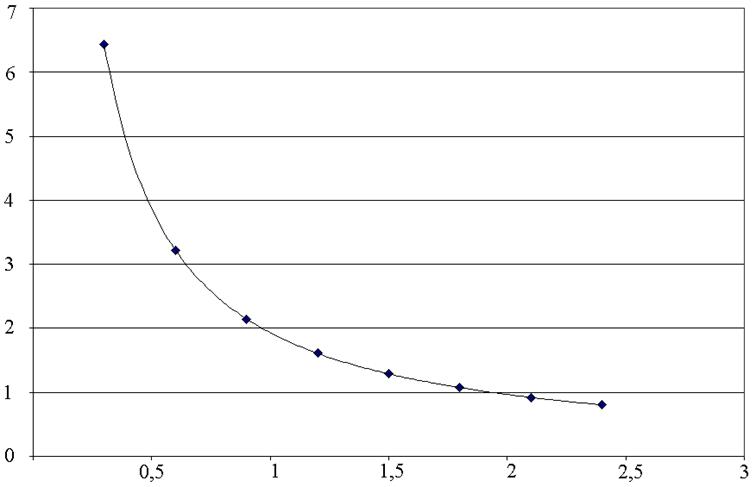
График зависимости a_n(t):

*10¹³ а_n, м/с²

t *10-7 с	an *1013 an
0,3	6,44
0,6	3,22
0,9	2,15
1,2	1,61
1,5	1,29
1,8	1,07
2,1	0,92
2,4	0,81

    *10^-7 t, c

Выводы по полученным результатам.

1)  Частица, влетающая в заряжённый конденсатор, и направленная под  углом к силовым линиям электрического поля, движется по криволинейной траектории.

2)  Можно считать, что заряженная частица внутри конденсатора движется только под действием электрических сил.

3)  Скорость частицы от ее координаты x зависит прямо пропорционально.

4)  Между нормальным ускорением частицы и временем её полета в конденсаторе существует обратно пропорциональная зависимость.