Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Кафедра общей и технической физики
Расчетно-графическое задание
Тема: «Кинематика материальной точки»
Вариант 23
Выполнил: студент гр. БА-02 ________________ /Михалов А.И./
(подпись) (Ф.И.О.)
Проверил: доцент ________________ /Смирнова Н.Н./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
1. Формулировка задания.
Кинематическое уравнение
движения материальной точки по прямой (ось x)
имеет вид, ![]()
Найти:
1. Путь, пройденный материальной точкой за интервал времени от t1=2.2с до t2=10с.
2. Среднюю путевую скорость V за тот же интервал времени.
3. Среднее значение ускорения.
4. Координату материальной точки в момент времени t1 и t2
Построить графики зависимостей величин V(t), а(t) при изменении времени.
2 Краткое теоретическое содержание.
Исходное уравнение – х=f(t)=7+3t-0,02t3 – уравнение зависимости координаты от времени. Данное уравнение является уравнением прямолинейного движения, т.к. изменяется только одна координата.
Материальная точка – тело, размерами которого можно пренебречь по сравнению с расстоянием до других тел.
Путь (S) – расстояние по траектории (от начала движения до данной точки). [S]=м
Скорость (![]() ) – векторная величина, которая
определяет как быстроту движения, так и его направление в данный момент времени.
Скорость – это первая производная радиус-вектора по времени. [V]=м/с
) – векторная величина, которая
определяет как быстроту движения, так и его направление в данный момент времени.
Скорость – это первая производная радиус-вектора по времени. [V]=м/с
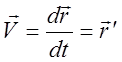
Среднепутевая скорость (![]() ) – физическая величина, которая
определяется отношением пути, пройденного точкой, к промежутку времени.
) – физическая величина, которая
определяется отношением пути, пройденного точкой, к промежутку времени.
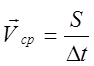
Ускорение (![]() ) – векторная физическая величина,
определяющая быстроту изменения скорости по модулю и направлению. Ускорение –
это вторая производная радиус-вектора по времени, или первая производная
скорости по времени. [a]=м/с2
) – векторная физическая величина,
определяющая быстроту изменения скорости по модулю и направлению. Ускорение –
это вторая производная радиус-вектора по времени, или первая производная
скорости по времени. [a]=м/с2
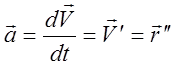
Среднее ускорение (аср) - физическая величина, которая равна отношению изменения скорости к интервалу времени.
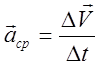
Равнозамедленное прямолинейное движение – движение, при котором скорость материальной точки за равные промежутки времени изменяется на одну и тужу величину, причём направления вектора скорости и ускорения противоположны.)
Основные формулы, применяемые в работе.
1. Путь, пройденный материальной точкой за интервал времени от t1до t2:
Для определения пути разобьем его на два, т.к. при изменении знака проекции скорости, точка изменяет направление движения и начинает двигаться в обратном направлении:
S=S1+S2;
где S1- путь, пройденный материальной точкой за время t max-t 1;
S2 - путь, пройденный материальной точкой за время t 2-t max;
t max– время в момент возврата материальной точки (когда точка начинает двигаться в обратном направлении: путь возрастает, а координата материальной точки убывает).
Чтобы найти формулы вычисления S1 и S2, схематично изобразим данное движение:
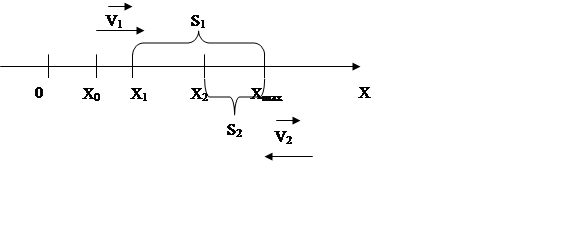 |
Рисунок 1.
Из данного рисунка видно, что путь равен приращению координаты:
S1=xmax-x1;
S2=xmax-x2;
где x1,x2 – координаты точки в моменты времени t 1 и t 2 соответственно;
xmax – максимальная координата, которую материальная точка достигает в момент, когда начинает двигаться обратно (скорость меняет знак).
![]()
2.
t max определяется приравниванием
к нулю первой производной от координаты по времени, т.к. по свойству максимума
в точке, в которой функция х=f(t)
максимальное значение, первая производная этой функции равна нулю. Т.к. при
данном движении все переменные изменяются только по координате Х, то приращение
(дифиренцал) радиус-вектора равно приращению (дифиренцалу) координаты (![]() ):
):
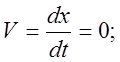
3. Средняя путевая скорость Vср за тот же интервал времени (в соответствии с определением):
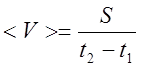
4. Среднее значение ускорения (в соответствии с определением):
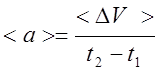
Т.к. скорость равна отношению приращения радиус вектора к интервалу времени, за которое это приращение произошло, то можно записать данную формулу следующим образом:
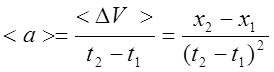
3 Решение:
Данное кинематическое уравнение
движения материальной точки ![]() соответствует
равнопеременному движению.
соответствует
равнопеременному движению.
3.1. Координаты материальной точки в моменты времени t 1 и t 2 определяются подстановкой соответствующих значений моментов времени:
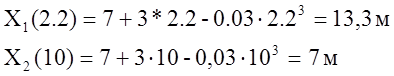
3.2. Для определения момента возврата найдём первую производную от координаты по времени.
![]()
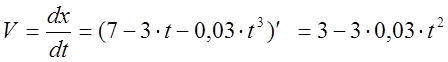
![]() Чтобы
определить момент возврата приравняем полученное выражение к нулю.
Чтобы
определить момент возврата приравняем полученное выражение к нулю.
![]()
![]()
3.3. Время в момент возврата материальной точки:
![]()
3.4. Максимальная координата
Подставив, значение момента возврата материальной точки в уравнение координаты определим:
![]()
3.5. Путь, пройденный материальной точкой за интервал времени от t1до t2:
S=2* xmax-x2- x1.
<S>=2*18.5-13.3-7=16.8м
3.6. Средняя путевая скорость Vср за тот же интервал:
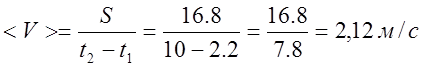
3.7. Среднее значение ускорения:
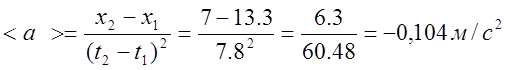
3.8. Графики зависимостей величин V(t), а(t):
Уравнение зависимости скорости от
времени уже найден в пункте 3.2 (![]() ). Он представляет
собой ветвь перевернутой параболы
). Он представляет
собой ветвь перевернутой параболы
График зависимости скорости от времени.
![]()
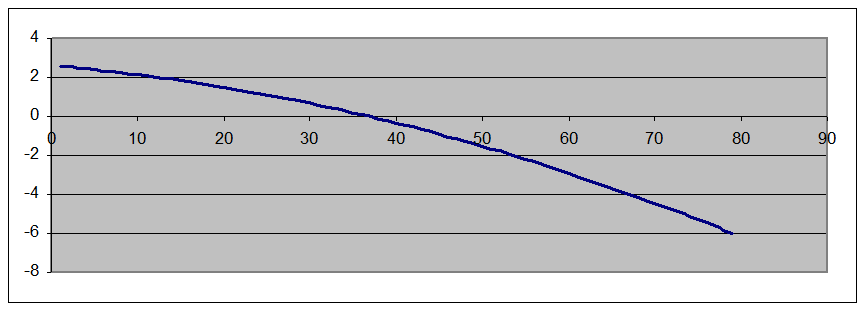
Потому что точка меняет направление движения в момент времени t=5,77 с., график зависимости скорости от времени пересекает ось Х.
Найдём уравнение мгновенного ускорения в произвольный момент времени t. Для этого возьмём вторую производную от координаты x:
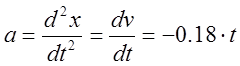
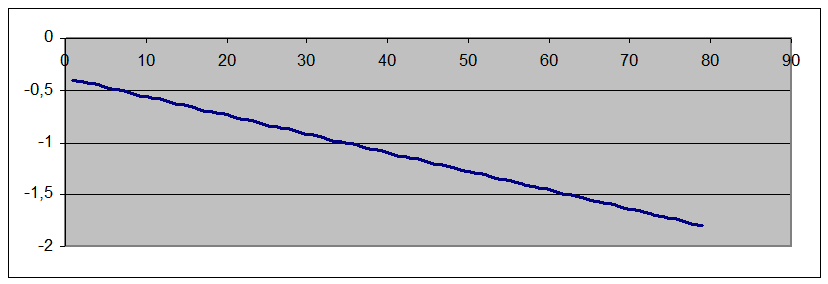
График зависимости а(t) представляет собой прямую. .
 |
Вывод: В расчетно-графическом задании “Кинематика материальной точки” рассматривалось движения материальной точки по прямой. В результате решения я нашёл:
1. <S>=16,8 м
2. ![]()
3. ![]()
4. X1=13,3 м; X2=7 м
Построенные графики отображают зависимость а(t) и V(t).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.