Санкт-Петербургский государственный горный институт
(технический университет)
Кафедра общей и технической физики
Лабораторная работа №7
Измерение диэлектрической проницаемости твердых материалов

Рис. 1. Измерительная установка: диэлектрическая проницаемость различных материалов
Санкт-Петербург
2008
Цель работы: Определение
электрической ёмкости конденсатора ![]() . Выявление взаимосвязи
электрической постоянной
. Выявление взаимосвязи
электрической постоянной ![]() и напряжения
и напряжения ![]() , электрической постоянной
, электрической постоянной ![]() и расстояния между обкладками конденсатора
и расстояния между обкладками конденсатора
![]() . Определение зависимости диэлектрической
проницаемости от напряжения
. Определение зависимости диэлектрической
проницаемости от напряжения ![]() .
.
Общие сведения.
Основные законы, явления и физические величины, изучаемые в работе: Уравнение Гаусса, условие потенциальности поля, электрическая постоянная, ёмкость плоского конденсатора, реальные заряды, нескомпенсированные заряды, электрическое смещение, диэлектрическая поляризация, диэлектрическая проницаемость.
Электростатические поле системы неподвижных точечных зарядов в вакууме (и с хорошей степенью приближения – в воздухе), описывается теоремой Гаусса (1) и условием потенциальности поля (2):
1. Поток вектора напряжённости электрического поля сквозь произвольную
неподвижную замкнутую поверхность, мысленно проведённому в электрическом поле,
равен отношению суммарного свободного заряда Q, заключённого внутри
области, ограниченной этой поверхностью к электрической постоянной ![]() :
:
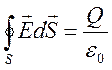 (1)
(1)
2. Циркуляция вектора напряжённости электрического поля по произвольному неподвижному замкнутому контуру ℓ, мысленно проведённому в электрическом поле равна нулю:
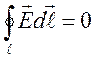 (2)
(2)
где ![]() – напряженность электрического поля.
– напряженность электрического поля.
Если электрический заряд равномерно распределён вдоль бесконечной плоскости, то поле её однородно. Вектор напряженности поля в любой точке имеет направление перпендикулярное к плоскости.
У плоскости конечных размеров поле будет однородным только для точек, расположенных на небольших, по сравнению с размерами плоскости, расстояниях и значительно отдалённых от её краёв.
Поле двух параллельных плоскостей, имеющих равные по модулю заряды, но противоположные по знаку, полностью сосредоточено между плоскостями. В области между плоскостями складываемые поля имеют одинаковые направления, и результирующая напряжённость удваивается. Вне объёма, ограниченного плоскостями, складываемые поля имеют противоположные направления и результирующая напряжённость равна нулю.
Система из двух проводников (обкладок), область между которыми заполнена диэлектриком малой толщины, по сравнению с размерами проводников, называется конденсатором. Плоский конденсатор состоит из двух равных по площади металлических пластин, расположенных на малом расстоянии d одна от другой.
Если на обкладки конденсатора подано напряжение Uc, то
между его пластинами появляется электрическое поле (см. рис. 2),
характеризующееся напряжённостью ![]() :
:
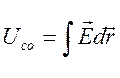 .
.
Благодаря электрическому полю электростатические заряды противоположных знаков притягиваются к поверхностям конденсатора. Поскольку источники напряжения не генерируют заряды, а только разделяют их, абсолютные величины противоположных по знаку электростатических зарядов должны быть равными.
Силовые линии электрического поля перпендикулярны поверхности плоского конденсатора. Вследствие симметрии, которая может быть экспериментально проверена для малых расстояний d между обкладками конденсатора, из уравнения (1) можно получить:
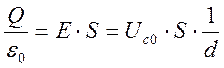 (3)
(3)
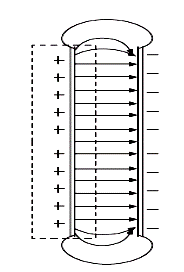
Рис. 2. Электрическое поле плоского конденсатора с малым, по сравнению с диаметром пластины, расстоянием между пластинами.
На рис.2 пунктиром указан объем, охватывающий только одну обкладку конденсатора, по которому производится интегрирование. Поскольку поверхность в пределах конденсатора может быть перемещена без изменения потока, поле в конденсаторе однородно. Напряженность электрического поля вне конденсатора равна нулю, потому что для произвольных объемов, охватывающих обе обкладки конденсатора, результирующая величина заряда внутри них равна нулю.
Заряд Q конденсатора, таким образом, пропорционален напряжению; коэффициент пропорциональности C называют ёмкостью конденсатора.
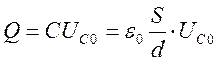 (4)
(4)
Ёмкость C конденсатора определяется только геометрическими параметрами конденсатора: прямо пропорциональна площади пластины и обратно пропорциональна расстоянию d между пластинами:
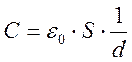 (5)
(5)
Для постоянного напряжения, с учетом возможности изменения расстояния
между пластинами, ёмкость является характеристикой количества заряда, который
может накопить конденсатор. Если значения U, Q, d и S
определены, то эти величины позволяют вычислять электрическую постоянную ![]() :
:
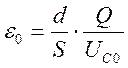 (6)
(6)
Точное значение этой величины ![]() = 8,8542×10-12 Ф/м. Уравнения (4),
(5) и (6) справедливы приблизительно – только в предположении, что силовые линии
поля параллельны. С увеличением расстояния между обкладками конденсатора
ёмкость уменьшается, что, в свою очередь, систематически приводит к слишком
большому значению электрической постоянной, определяемой по уравнения (6).
Поэтому величина электрической постоянной должна определяться для малого и
постоянного расстояния между пластинами (см. рис. 2).
= 8,8542×10-12 Ф/м. Уравнения (4),
(5) и (6) справедливы приблизительно – только в предположении, что силовые линии
поля параллельны. С увеличением расстояния между обкладками конденсатора
ёмкость уменьшается, что, в свою очередь, систематически приводит к слишком
большому значению электрической постоянной, определяемой по уравнения (6).
Поэтому величина электрической постоянной должна определяться для малого и
постоянного расстояния между пластинами (см. рис. 2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.