Измерение диэлектрической проницаемости твердых материалов, страница 3

Произведение вектора напряжённости электрического поля на диэлектрическую проницаемость диэлектрика и электрическую постоянную называется электрическим смещением  или электрической индукцией, причем линии этой величины начинаются и заканчиваются на реальных зарядах. Единицей электрического смещения служит кулон на квадратный метр (Кл/м²). Теорема Гаусса для диэлектрической среды в этом случае формулируется следующим образом:

Поток смещения электростатического поля сквозь произвольную замкнутую поверхность, проведённую в поле, равен алгебраической сумме свободных зарядов , охватываемых этой поверхностью:

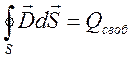                                                             (11)

В изотропной диэлектрической среде вектор  поляризованности пропорционален напряжённости электрического поля . Три физические величины – напряженность электрического поля , электрическое смещение  и поляризованность  связанны друг с другом следующим уравнением:

                                                      (12)

Если реальные заряды Q остаются на конденсаторе неизменными при помещении диэлектрика между пластинами, то согласно определению (3), напряжение  между пластинами понижается по сравнению с напряжением  в вакууме (или с хорошим приближением, в воздухе) в соответствии со значением диэлектрической проницаемости:

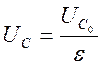                                                                  (13)

Точно так же из определения емкости (4) можно получить:

                                                                  (14)

где   – ёмкость конденсатора без диэлектрика. Общая форма уравнения (4) таким образом, принимает вид:

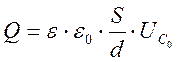                                                           (15)

Измерительная установка и электрическая схема.

Рис. 4. Измерительная установка: диэлектрическая проницаемость различных материалов

(1 – плоский конденсатор, диаметр пластин d = 260 мм; 2 – источник питания, высоковольтный, диапазон 0 ÷ 10 кВ; 3 – универсальный измерительный усилитель; 4 – вольтметр, 0,3 ÷ 300 В, 10 ÷ 300 В, переменный ток; 5 – конденсатор, ёмкость С = 218 нФ; 6 – пластмассовая пластинка: размеры 283 ´ 283 мм, площадь  S = 0.08 м², толщина d= 0.98 см; 7 – соединительные шнуры)

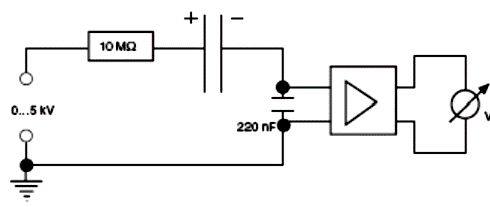
Рис.5. Электрическая схема

Хорошо изолированная пластина конденсатора переменной ёмкости , соединена с верхним выводом источника высокого напряжения через защитный резистор 10 МОм.

Средний вывод высоковольтного источника напряжения и противоположная обкладка конденсатора заземлены через конденсатор, ёмкостью С = 220 нФ. Измерительный усилитель устанавливается в режим высокого входного сопротивления, коэффициент усиления 1, константа времени 0. Входное сопротивление усилителя можно считать бесконечно большим. Усилитель необходим для того, чтобы конденсатор не разрядился через вольтметр. Для облегчения расчёта составим эквивалентную электрическую схему:

 

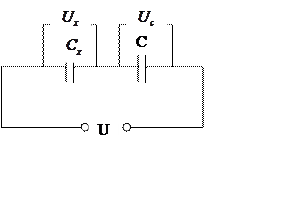Рис.6 Эквивалентная электрическая схема

При последовательном соединении конденсаторов  и , заряды на них равны, напряжения складываются. Исходя из этого, составим систему уравнений:

                                                             (16)

.

Из системы уравнений (16) выразим :

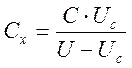                                                               (17)

Из формулы (5) для ёмкости воздушного конденсатора и формулы (14) для конденсатора с диэлектриком получим общее выражение:

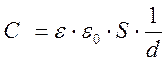.                                                        (18)

Таким образом, теоретическое значение  можно определить, зная геометрические параметры конденсатора и диэлектрические свойства материала, заполняющего промежуток между обкладками конденсатора:

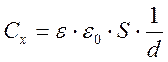                                                         (19)

Электрическую постоянную можно выразить, приравняв формулы (17) и (19):

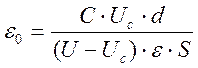.                                                    (20)