Санкт-Петербургский государственный горный институт
(технический университет)
Кафедра общей и технической физики
Лабораторная работа №8
Измерение низких сопротивлений материалов

Рис. 1. Снятие вольт-амперной характеристики металлического прута.
Санкт-Петербург
2008
Цель работы: Определение удельного сопротивления, контактного сопротивления, и удельной теплопроводности металлов низкоомных материалов с помощью измерительного усилителя.
Общие сведения
Экспериментальные законы и электронная теория. В основе классической электронной теории металлов, развитой Друде и Лоренцом, лежит представление об электронном газе, состоящем из свободных (коллективизированных) электронов. Электронному газу приписываются свойства идеального газа, т.е. движение электронов подчиняется законам классической статистики. Если считать, что атомы в металле ионизированы однократно, то концентрация свободных электронов будет равна концентрации атомов и может быть рассчитана по формуле
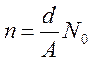 , (1)
, (1)
где d
– плотность материала; А – атомная масса; ![]() –
число Авогадро.
–
число Авогадро.
В соответствии с атомно-кинетической теорией идеальных газов средняя кинетическая энергия электронов, находящихся в состоянии непрерывного хаотического движения, линейно возрастает с температурой:
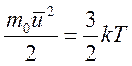 (2)
(2)
где ![]() –
средняя скорость теплового движения; k – постоянная
Больцмана. Температуре 300 К соответствует
средняя скорость порядка
–
средняя скорость теплового движения; k – постоянная
Больцмана. Температуре 300 К соответствует
средняя скорость порядка ![]() м/с, m0 – масса электрона.
м/с, m0 – масса электрона.
Приложение внешнего напряжения приводит к увлечению электронов в направлении действующих сил поля, т.е. электроны получают некоторую добавочную скорость направленного движения, благодаря чему и возникает электрический ток. Плотность тока в проводнике определяется выражением
![]() (3)
(3)
где e
– заряд электрона, ![]() – средняя скорость направленного
движения носителей заряда (скорость дрейфа).
– средняя скорость направленного
движения носителей заряда (скорость дрейфа).
В медном
проводнике плотности тока ![]()
![]() соответствует
скорость дрейфа электронов порядка
соответствует
скорость дрейфа электронов порядка ![]() , т.е. можно считать,
что в реальных условиях выполняется равенство
, т.е. можно считать,
что в реальных условиях выполняется равенство ![]() .
.
В промежутках между столкновениями с узлами решетки электроны при воздействии электрического поля движутся с ускорением
![]() .
.
Максимальная скорость дрейфа, приобретаемая электроном к концу свободного пробега,
![]() ,
,
где ![]() – время
свободного пробега.
– время
свободного пробега.
После столкновения для большинства электронов скорость направленного движения падает до нуля, т.е. накопленная кинетическая энергия передается атомам решетки. Поэтому среднее значение скорости дрейфа за время свободного пробега равно половине максимального:
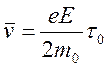 .
.
Поскольку ![]() , то при расчете времени свободного пробега
добавку скорости
, то при расчете времени свободного пробега
добавку скорости ![]() можно не учитывать:
можно не учитывать:
![]() ,
,
где ![]() –
средняя длина свободного пробега электронов.
–
средняя длина свободного пробега электронов.
Подстановка полученных соотношений в формулу для плотности тока приводит к следующему результату:
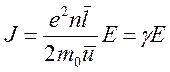 , (4)
, (4)
т.е. плотность тока пропорциональна напряженности электрического поля, а это есть аналитическое выражение закона Ома.
Таким образом, в рамках классической теории выражение для удельной электропроводности:
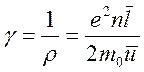 . (5)
. (5)
Представления о свободных электронах позволяет легко прийти к экспериментальному закону Видемана – Франца, устанавливающему связь между проводимостью и теплопроводностью металла. Электроны в металле переносят не только электрический заряд, но и выравнивают в нем температуру, обеспечивая высокую теплопроводность. Благодаря высокой концентрации свободных электронов, электронная теплопроводность преобладает над другими механизмами переноса теплоты. В соответствии с атомно-кинетической теорией идеального газа электронная теплопроводность может быть записана в виде
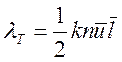 .
.
Поделив это выражение на удельную проводимость, найденную из (4), с учетом формулы (2) получим
![]() ,
(6)
,
(6)
т.е. отношение удельной
теплопроводности к удельной проводимости металла при данной температуре есть
величина постоянна, не зависящая от природы проводника. Отсюда, в частности,
следует, что хорошие проводники электрического тока являются и хорошими
проводниками теплоты. Константа ![]() получила название числа
Лоренца.
получила название числа
Лоренца.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.