I.Задание в соответствии с вариантом.
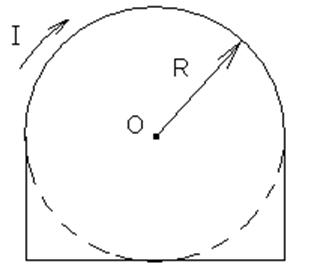
По плоскому контуру из
тонкого провода течёт ток ![]() . Радиус изогнутой части
контура R=90см=0,9м. Определить значение магнитной индукции
поля, создаваемого этим током в точке О.
. Радиус изогнутой части
контура R=90см=0,9м. Определить значение магнитной индукции
поля, создаваемого этим током в точке О.
Построить графики зависимости магнитной индукции от:
- силы тока I
- радиуса изогнутой части R.
II. Краткое теоретическое содержание.
1. Явление, изучаемое в РГР.
В данной РГР изучается магнитное поле, создаваемое контуром с током.
Магнитным полем называется одна из форм проявления электромагнитного поля. Магнитное поле действует только на движущиеся электрически заряженные частицы и тела, на проводники с током и на частицы и тела, обладающие магнитными моментами.
Магнитное поле создается проводниками с током, движущимися электрически заряженными частицами и телами, обладающими магнитными моментами, а также изменяющимися во времени электрическим полем.
2. Определение основных физических понятий, объектов, процессов и величин.
Силовой характеристикой
магнитного поля служит вектор магнитной индукции ![]() (вектор
индукции магнитного поля).
(вектор
индукции магнитного поля).
Вектор ![]() можно ввести одним из трёх эквивалентных
способов:
можно ввести одним из трёх эквивалентных
способов:
а) исходя из силового действия магнитного поля на движущуюся в нем заряженную частицу – точечный электрический заряд;
б) основываясь на силовом действии магнитного поля на малый элемент проводника с током;
в) исходя из силового действия магнитного поля на небольшую рамку с током.
На электрически
заряженную частицу, движущуюся в магнитном поле со скоростью ![]() , действует сила Лоренца
, действует сила Лоренца ![]() , которая направлена перпендикулярно к
вектору
, которая направлена перпендикулярно к
вектору ![]() .Отношение
.Отношение 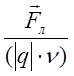 , где q – заряд
частицы, не зависит, как показывает опыт, ни от q, ни от
, где q – заряд
частицы, не зависит, как показывает опыт, ни от q, ни от ![]() . При изменении направления скорости
частицы в рассматриваемой точке сила Лоренца изменяется от нуля до значения
. При изменении направления скорости
частицы в рассматриваемой точке сила Лоренца изменяется от нуля до значения ![]() , связанного с магнитной индукцией
, связанного с магнитной индукцией ![]() в этой точке поля соотношением
в этой точке поля соотношением 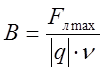 , (1)
, (1)
Итак, магнитная
индукция численно равна отношению силы, действующей на заряженную частицу со
стороны магнитного поля, к произведению абсолютной величины заряда и скорости
частицы таково, что эта сила максимальна. Вектор ![]() направлен
перпендикулярно к вектору силы
направлен
перпендикулярно к вектору силы ![]() , действующей на
положительно заряженную частицу (q>0), и вектору скорости
, действующей на
положительно заряженную частицу (q>0), и вектору скорости ![]() частицы
так, что из конца вектора
частицы
так, что из конца вектора ![]() вращения по кратчайшему
расстоянию от направления силы
вращения по кратчайшему
расстоянию от направления силы ![]() к направлению скорости
к направлению скорости ![]() видно происходящим против часовой стрелки.
Иначе говоря, векторы
видно происходящим против часовой стрелки.
Иначе говоря, векторы ![]() ,
, ![]() и
и ![]() образуют правую тройку.
образуют правую тройку.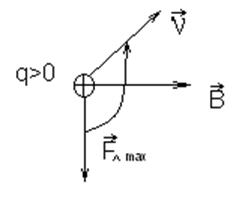
Для графического
изображения магнитного поля пользуются методом линий магнитной индукции
(силовыми линиями магнитного поля) называются линии, проведенные в магнитном
поле так, что в каждой точке поля касательная к линии магнитной индукции
совпадает с направлением вектора ![]() . Линии магнитной
индукции нигде не обрываются , т.е. не начинаются и не кончаются. Они либо
замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно
навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не
возвращаются вторично в любую точку поверхности. Последний случай
осуществляется, например, в магнитном поле, создаваемом системой из кругового
тока и бесконечного прямолинейного проводника с током, проходящего через центр
кругового витка с током, перпендикулярно к его плоскости.
. Линии магнитной
индукции нигде не обрываются , т.е. не начинаются и не кончаются. Они либо
замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно
навиваются на некоторую поверхность, всюду плотно заполняя её, но никогда не
возвращаются вторично в любую точку поверхности. Последний случай
осуществляется, например, в магнитном поле, создаваемом системой из кругового
тока и бесконечного прямолинейного проводника с током, проходящего через центр
кругового витка с током, перпендикулярно к его плоскости.
3. Законы и соотношения, описывающие изучаемые процессы.
Для магнитного поля справедлив принцип суперпозиции: магнитная индукция поля произвольной системы проводников с токами равна геометрической сумме магнитных индукций полей малых элементов этих проводников.
Согласно закону
Био-Савара-Лапласа магнитная индукция ![]() поля в
вакууме малого элемента длиной
поля в
вакууме малого элемента длиной ![]() , по которому протекает
постоянный ток
, по которому протекает
постоянный ток ![]() , равна
, равна 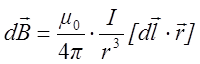 ,
(2), где
,
(2), где ![]() -радиус - вектор, проведенный из элемента
проводника в рассматриваемую точку поля;
-радиус - вектор, проведенный из элемента
проводника в рассматриваемую точку поля; ![]()
![]() - магнитная постоянная. Направление
вектора
- магнитная постоянная. Направление
вектора ![]() можно найти по правилу Максвелла(правилу
Буравчика): если ввинчивать буравчик с правой резьбой по направлению тока в
элементе проводника, то направление движения рукоятки буравчика укажет
направление вектора
можно найти по правилу Максвелла(правилу
Буравчика): если ввинчивать буравчик с правой резьбой по направлению тока в
элементе проводника, то направление движения рукоятки буравчика укажет
направление вектора ![]() магнитной индукции.
магнитной индукции.
Из закона
Био-Савара-Лапласа следует, что модуль вектора ![]() равен
равен 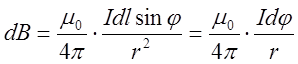 , (3), где
, (3), где ![]() - угол,
под которым виден из рассматриваемой точки поля элемент
- угол,
под которым виден из рассматриваемой точки поля элемент ![]() проводника
с током;
проводника
с током; ![]() - угол между векторами
- угол между векторами ![]() и
и ![]() .
.
Рассматриваемый в настоящей РГР контур состоит из трех отрезков прямолинейного проводника с током и половины кругового проводника. Индукции магнитных полей таких проводников получается из закона Био-Савара-Лапласа путём интегрирования.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.