Санкт-Петербургский государственный горный институт
(технический университет)
Кафедра общей и технической физики
Лабораторная работа №10
Исследование влияния температуры на характеристики различных материалов и диодов

Рис.1. Фотография экспериментальной установки
Санкт-Петербург
2008
Цель работы: 1. Изучение влияния температуры на сопротивление различных материалов. 2. Определение температурных коэффициентов.
Общие сведения.
Электрическое сопротивление – основная
электрическая характеристика проводника; величина, характеризующая
противодействие электрической цепи или ее участка электрическому току.
Электрическое сопротивление обусловлено преобразованием электрической энергии в
другие виды энергии. Для однородного цилиндрического проводника длиной ![]() и площадью поперечного сечения S сопротивление определяется по формуле:
и площадью поперечного сечения S сопротивление определяется по формуле:
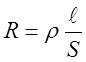
где ![]() – удельное сопротивление цилиндрического
проводника,
– удельное сопротивление цилиндрического
проводника, ![]() . Единицей электрического сопротивления
проводников служит Ом. Сопротивлением в 1 Ом обладает такой участок цепи,
в котором при напряжении 1 В возникает ток силой 1 А.
. Единицей электрического сопротивления
проводников служит Ом. Сопротивлением в 1 Ом обладает такой участок цепи,
в котором при напряжении 1 В возникает ток силой 1 А.
Проводник, обладающий электрическим сопротивлением, называется резистором.
![]() Электронная теория
проводимости. Смысл электронной теории
проводимости сводится к тому, что каждый атом металла отдает валентный электрон
из внешней оболочки кристаллической решётке. Свободные электроны растекаются по
металлу, образуя некое подобие отрицательно заряженного газа. Атомы металла при
этом объединены в трехмерную кристаллическую решетку, которая практически не
препятствует перемещению свободных электронов. Принято считать, что длина
свободного пробега электронов в металле
Электронная теория
проводимости. Смысл электронной теории
проводимости сводится к тому, что каждый атом металла отдает валентный электрон
из внешней оболочки кристаллической решётке. Свободные электроны растекаются по
металлу, образуя некое подобие отрицательно заряженного газа. Атомы металла при
этом объединены в трехмерную кристаллическую решетку, которая практически не
препятствует перемещению свободных электронов. Принято считать, что длина
свободного пробега электронов в металле ![]() соизмерима
с расстоянием между соседними узлами кристаллической решётки
соизмерима
с расстоянием между соседними узлами кристаллической решётки ![]() . Как только к проводнику прикладывается
электрическая разность потенциалов, свободные электроны
. Как только к проводнику прикладывается
электрическая разность потенциалов, свободные электроны 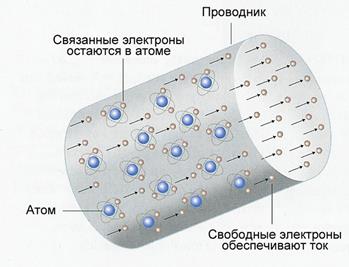 приходят в упорядоченное движение. До столкновения с
атомами кристаллической решетки электроны движутся равноускоренно и перестают
ускоряться, сталкиваясь с атомами решетки. В результате скорость электронов
устанавливается на некоей усредненной отметке, которая называется скоростью
миграции, или дрейфовой скоростью. Эта скорость не высока. Например,
в обычной бытовой электропроводке средняя скорость миграции электронов
составляет всего несколько миллиметров в секунду. Но время установления тока
зависит от скорости распространения поля, вызывающего движение заряженных
частиц. Так как эта скорость равна скорости света С (С =
приходят в упорядоченное движение. До столкновения с
атомами кристаллической решетки электроны движутся равноускоренно и перестают
ускоряться, сталкиваясь с атомами решетки. В результате скорость электронов
устанавливается на некоей усредненной отметке, которая называется скоростью
миграции, или дрейфовой скоростью. Эта скорость не высока. Например,
в обычной бытовой электропроводке средняя скорость миграции электронов
составляет всего несколько миллиметров в секунду. Но время установления тока
зависит от скорости распространения поля, вызывающего движение заряженных
частиц. Так как эта скорость равна скорости света С (С = ![]() ), то все свободные электроны начинают
двигаться практически одновременно. Время
установления электрического тока в цепи длиной L
равно
), то все свободные электроны начинают
двигаться практически одновременно. Время
установления электрического тока в цепи длиной L
равно 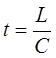 . Атомы
кристаллической решетки испытывают соударения с электронами, получают от них
дополнительную энергию и начинают колебаться с большей амплитудой относительно
условной точки покоя, вследствие чего проводник нагревается.
. Атомы
кристаллической решетки испытывают соударения с электронами, получают от них
дополнительную энергию и начинают колебаться с большей амплитудой относительно
условной точки покоя, вследствие чего проводник нагревается.
Электронная теория проводимости хорошо описывает некоторые основные явления из области электропроводности, но не может описать многие их особенности. В частности, она не может объяснить явление сверхпроводимости. Поэтому сегодня электропроводящие свойства вещества принято объяснять в рамках квантовой механики.
Элементы квантовой теории проводимости. Электроны, как и другие элементарные частицы, обладают свойством корпускулярно-волнового дуализма. Поэтому движение свободных электронов в металле можно рассматривать как распространение плоских электронных волн, длина которых определяется соотношением де Бройля:
![]()
Такая плоская волна в строго периодическом
потенциальном поле распространяется без рассеяния энергии. Рассеяние,
приводящее к появлению сопротивления, возникает в тех случаях, когда в решётке
имеются нарушения структуры. Эффективное рассеяние волн наблюдается, если
размеры дефектов превышают четверть длины волны. В металлах энергия электронов
проводимости соответствует (3 – 15) эВ. Этой энергии соответствует длина волны (3 – 5)![]() м. Поэтому любые микронеоднородности структуры препятствуют
распространению электронных волн, вызывая рост удельного сопротивления металла.
м. Поэтому любые микронеоднородности структуры препятствуют
распространению электронных волн, вызывая рост удельного сопротивления металла.
Рассмотрим упрощённую модель. Пусть
интенсивность рассеяния прямо пропорциональна поперечному сечению сферического
объёма, который занимает колеблющийся атом, а площадь поперечного сечения
пропорциональна квадрату амплитуды тепловых колебаний ![]() .
Тогда для длины свободного пробега электронов можно записать:
.
Тогда для длины свободного пробега электронов можно записать:
![]() (1)
(1)
где N – число атомов в единице объёма.
Потенциальная энергия атома, отклонённого от
узла решётки на ![]() определяется:
определяется:
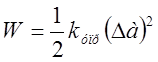
где ![]() – коэффициент упругости.
– коэффициент упругости.
Средняя энергия гармонического осциллятора
равна ![]() , тогда:
, тогда:
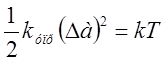
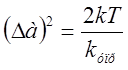 (2)
(2)
Решая совместно выражения (2) и (1) получим:
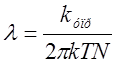
Длина свободного пробега обратно пропорциональна температуре.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.