Для того, чтобы описать распределение вероятности нахождения
частицы в данный момент времени в некоторой точке пространства, вводят функцию ![]() , называемую волновой функцией.
, называемую волновой функцией.
Физический смысл имеет не сама функция ![]() , а квадрат ее модуля
, а квадрат ее модуля ![]() , где
, где ![]() -
функция, комплексно сопряженная с
-
функция, комплексно сопряженная с ![]() . Величина
. Величина ![]() имеет смысл плотности вероятности, т.
е. определяет вероятность пребывания частицы в данной точке пространства.
имеет смысл плотности вероятности, т.
е. определяет вероятность пребывания частицы в данной точке пространства.
Функции ![]() , удовлетворяющие
уравнению Шредингера при данном значении U
(потенциальная энергия частицы в силовом поле), называются собственными
функциями. Значения Е (полной энергии частиц), при которых
существуют решения уравнения Шредингера, называются собственными значениями.
, удовлетворяющие
уравнению Шредингера при данном значении U
(потенциальная энергия частицы в силовом поле), называются собственными
функциями. Значения Е (полной энергии частиц), при которых
существуют решения уравнения Шредингера, называются собственными значениями.
Уравнение Шредингера: 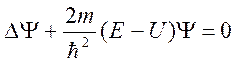 .
.
Отношение квантов модулей амплитуд отраженной и падающей волн определяет вероятность отражения частицы от потенциального барьера и называется коэффициентом отражения.
Отношение квантов модулей амплитуд прошедшей и падающей волн определяет вероятность прохождения частицей потенциального барьера и называется коэффициентом отражения.
Собственное значение энергии
частицы: 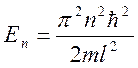 ,
,
где n – главное квантовое число, n = 1, 2, 3…;
![]() – постоянная Планка,
– постоянная Планка, ![]() ;
;
m – масса электрона, ![]() ;
;
l – ширина потенциальной ямы, м.
Волновая функция: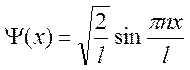 , где х – координата частицы, м.
, где х – координата частицы, м.
Вероятность пребывания частицы в
области (0, l): 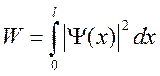 .
.
Среднее значение координаты частицы
в области (0, l): 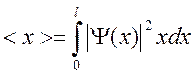 .
.
Коэффициент отражения (при ![]() ):
): 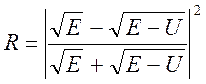 ,
,
где Е – энергия частицы, эВ.
U – высота потенциального барьера, эВ.
Коэффициент прозрачности (при ![]() ):
):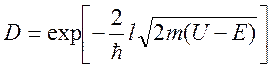 ,
,
где l – ширина потенциального барьера, м.
Связь между R
и D: ![]()
Исходные данные – Вариант №3:
![]() ;
; ![]() ;
; 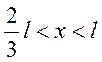 .
.
Электрон находится в потенциальной яме с бесконечно высокими стенками и шириной l. При заданных n:
1) построить графики собственных функций;
2) построить графики плотности вероятности обнаружения частицы в интервале [0; l];
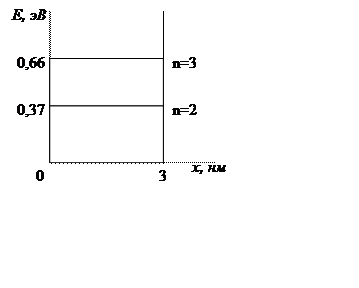
3) найти собственные значения энергии частицы. Изобразить схематически в удобном масштабе энергетические уровни с указанием полученных значений энергии;
4) найти вероятность пребывания частицы в указанной области;
5) найти среднее значение координаты частицы в указанной области квантовой ямы.
 |
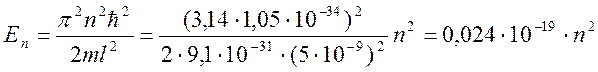
![]()
![]()
Энергетические уровни:
 |
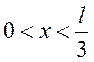
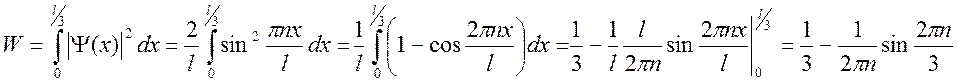
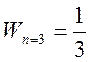
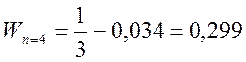
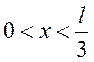
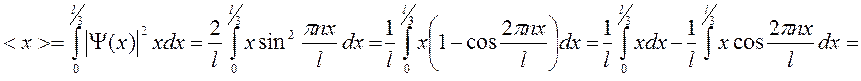
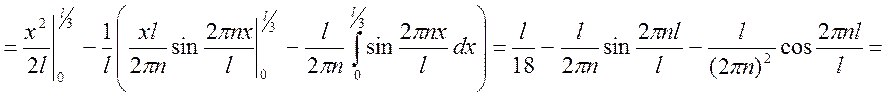
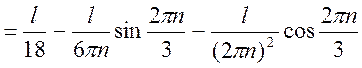
![]()
![]()
На каждом энергетическом уровне число полуволн соответствует значению главного квантового числа.
Плотность вероятности представляет собой квадрат (по модулю) волновой функции. Она не может иметь отрицательное значение.
Из пункта 3) можем видеть, что энергия частицы на четвертом уровне почти в два раза больше, чем на третьем.
Так как на четвертом уровне в точке 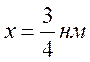 плотность
вероятности равна нулю, то уменьшается вероятность нахождения частицы в области
плотность
вероятности равна нулю, то уменьшается вероятность нахождения частицы в области
![]() по сравнению с третьим уровнем.
по сравнению с третьим уровнем.
При расчете средней координаты можно было ожидать, что ее
значение будет находиться в пределах ![]() . Результаты
соответствуют этому. Причем на четвертом уровне средняя координата находится
левее, т. к. имеется нулевая плотность вероятности в точке
. Результаты
соответствуют этому. Причем на четвертом уровне средняя координата находится
левее, т. к. имеется нулевая плотность вероятности в точке 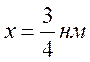 .
.
Электрон с энергией Е проходит сквозь потенциальный барьер высотой U. Определить вероятность:
1) прохождения частицы сквозь потенциальный барьер;
2) отражения частицы от потенциального барьера.
![]()
![]()
Т. к. ![]() ,
то расчитываем D:
,
то расчитываем D:
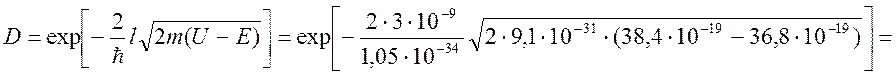
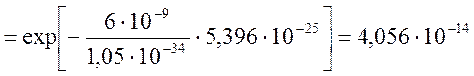
Т. к. ![]() , то
, то
![]() .
.
Так как энергия частицы меньше потенциального барьера, то вероятность ее отражения должна быть больше вероятности прохождения. Судя по найденным коэффициентам, частица скорее всего отразится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.