Заряженная частица в однородной потенциальной яме

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт им. Г.В. Плеханова

(технический университет)

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

Вариант 5

По дисциплине:                                          Физика

Тема:                    Заряженная частица в однородной потенциальной яме

Выполнил: студент  гр. НБ-03     ________________     / Горный Т.В./

                                                                                                     (подпись)                                   (Ф.И.О.)

ОЦЕНКА: ______________

Дата: __________________

ПРОВЕРИЛ:

Руководитель:          _________________            / Смирнова Н.Н./

                                                                     (подпись)                                                  (Ф.И.О.)

Санкт-Петербург

2005 г.

Формулировка задания:

         Заряженная частица, движется в однородной потенциальной «яме» шириной l с бесконечно высокими «стенками» при термодинамической температуре T. Уравнение Шредингера имеет вид:

 

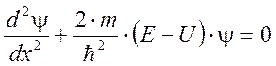
         Решить уравнение Шредингера для частицы находящейся внутри однородной потенциальной «ямы».

Построить графики зависимостей:

1. Полной энергии от главного квантового числа.

2. Вероятность обнаружения частицы внутри «ямы».

Параметры частицы:

- потенциальная энергия частицы

- кинетическая энергия частицы

 - ширина однородной потенциальной ямы

- термодинамическая температура

Краткое теоретическое содержание:

Явление, изучаемое в расчетно-графической работе - волновые функции частиц, определяющих состояние частиц, движущихся в различных силовых полях, определяются с помощью уравнения Шредингера.

Собственные значения энергии – это избранные значения энергии, при которых дифференциальное уравнение (1) имеет решение.

Собственные функции задачи – решения, соответствующие собственным значениям энергии.

Спектр величины – совокупность собственных значений.

Дискретный спектр – совокупность собственных значений, образующих дискретные значения.

Сплошной (непрерывный) спектр – собственные значения, образующие непрерывную последовательность.

         Уравнение Шредингера позволяет найти волновую функцию данного состояния и определить вероятность нахождения частицы в различных точках пространства

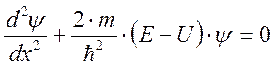    (1)

 - координатная (амплитудная) часть волновой функции;

m – масса частицы [кг];

Е – полная энергия частицы [Дж];

U – потенциальная энергия [Дж];

1,05∙10^-34 Дж∙с - постоянная Планка

         Стенки потенциальной ямы считаются непроницаемыми и находящимися на оси х в точках  и , движение частицы в яме одномерное.

         За пределы ямы частица выйти не может, поэтому вероятность обнаружения частицы

вне ямы равна 0. Из условия непрерывности следует, что  должна быть равна нулю и на границах ямы, т.е. что

В области, где  не равна тождественно нулю, уравнение (1) имеет вид

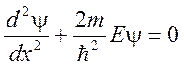
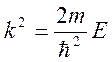В этой области . Вводим обозначения . Получим уравнение .

Решение такого уравнения имеет вид , где А – константа

Из условия  получаем:

Также должно выполняться условие:

где - главное квантовое число

Собственное значение энергии частицы: 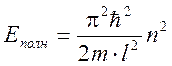       (2)

Спектр энергии – дискретный. Схема энергетических уровней будет выглядеть:

 

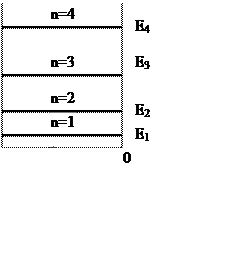В соответствии со смыслом волновой функции вероятность того, что частица окажется в пределах объема dV равна .

Для нахождения коэффициента А воспользуемся условием нормировки: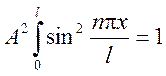

На концах промежутка интегрирования подынтегральная функция обращается в 0. Поэтому значение интеграла можно получить, умножив среднее значение 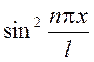 (равное 1/2) на длину промежутка . Получим: , откуда .

Таким образом собственные функции имеют вид: 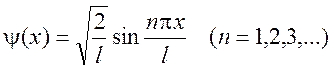(3)

Термодинамическую температуру находим из формулы: 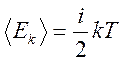    (4)

 - средняя кинетическая энергия молекулы;

i – число степеней свободы

(i=3 для одноатомной молекулы, i=5 для двухатомной и i=6 для трех- и более атомной молекулы);

В нашем случае , поскольку   ¹²¹Sb⁺  - одноатомная молекула

– постоянная Больцмана;

Т – термодинамическая температура, [K].

Решение:

С помощью уравнения (2) находим полную энергию:

  

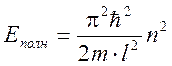
В нашем случае: ¹²¹Sb⁺, ,

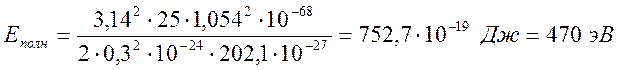
Поскольку , то:

С помощью уравнения (4) находим термодинамическую температуру:

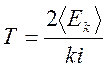
Поскольку   ¹²¹Sb⁺  - одноатомная молекула -

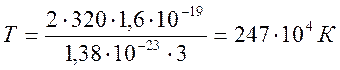
Из уравнения (3):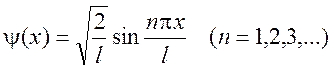

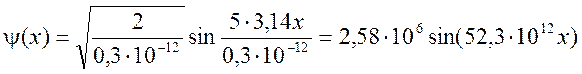
Из уравнения (2):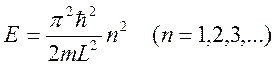

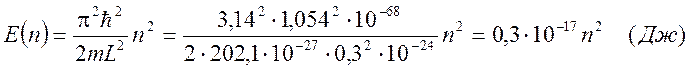
Вероятность обнаружения частицы в координате х в одномерной потенциальной яме:

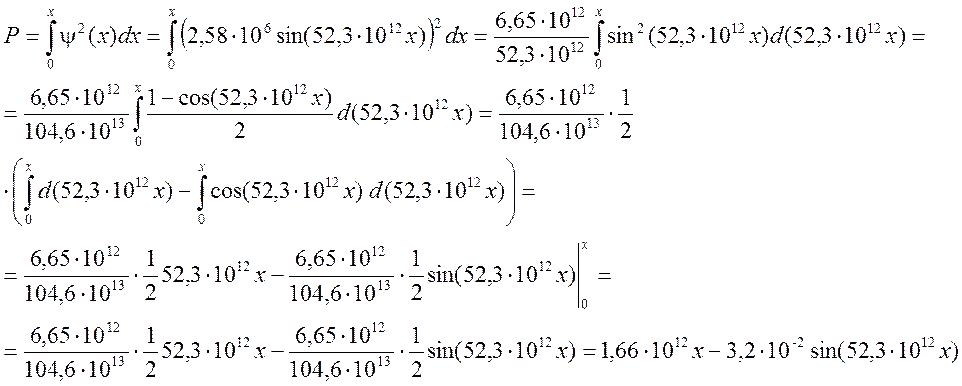
 Проверка размерности:

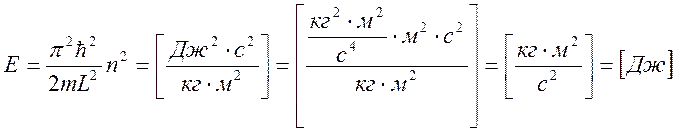
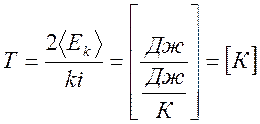
Графический материал:

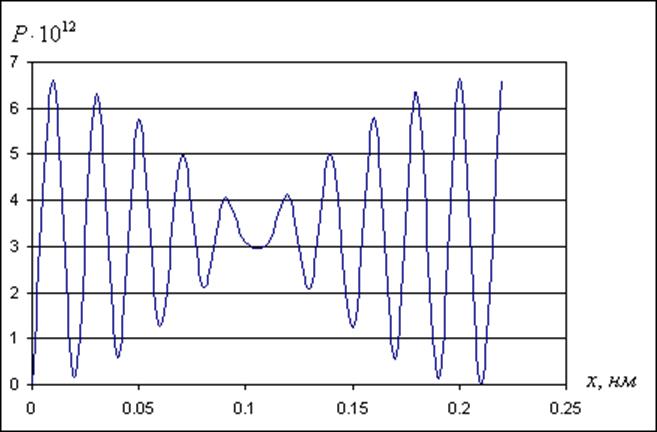
1. График вероятности обнаружения частицы в потенциальной яме:

0	0
0.01	7
0.02	0
0.03	6
0.04	1
0.05	6
0.06	1
0.07	5
0.08	2
0.09	4
0.1	3
0.11	3
0.12	4
0.13	2
0.14	5
0.15	1
0.16	6
0.17	1
0.18	6
0.19	0
0.2	7
0.21	0
0.22	7

                                                                                                                                             

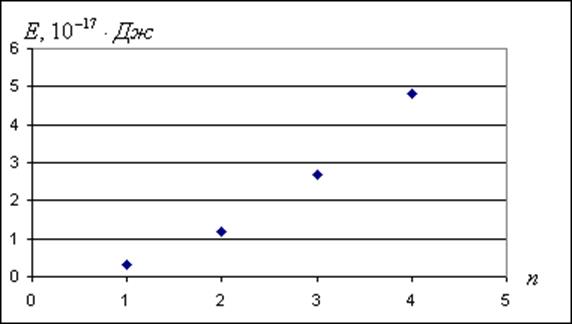
2. График зависимости полной энергии от главного квантового числа:

1	0.3
2	1.2
3	2.7
4	4.8

                                               

Вывод: заряженная частица ¹²¹Sb⁺, движется в однородной потенциальной «яме» шириной  с бесконечно высокими «стенками» при термодинамической температуре . Ее кинетическая энергия , а потенциальная . В ходе проделанной работы были построены графики зависимости полной энергии от главного квантового числа и вероятности обнаружения частицы в потенциальной яме. Из графика вероятности обнаружения частицы в потенциальной яме можно сделать вывод, что частица не может быть обнаружена в середине ямы и вместе с тем она одинаково часто бывает как в левой, так и в правой половине ямы.