Економетрика: Навчальний посібник (Уведення. Розділ "Моделі з двома перемінними"), страница 8

                                    (1.11)

Прологарифмировав (1.11), одержуємо

ln = ln a₀ + a₁ ln + U,

і рівняння

 =  + а₁ ln  + U,       =ln            (1.12)

стає лінійним щодо параметрів = ln a₀  і а₁, а також обурення U.

Приклад 3Функція

 =   (а₀  > 0, а₁  > 0)                       (1.13)

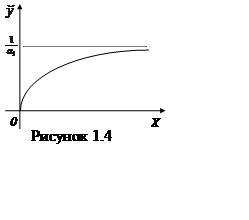може моделювати вплив витрат Х перемінного ресурсу R на випуск Y продукції, якщо рівень випуску не може бути більше деякої преде-льной розміру. Крива (1.13) явля-ется увігнутої. При відсутності витрат випуск дорівнює нулю. Якщо X → ∞, , тобто при необмеженому воз-растании витрат Х випуск Y не може бути більше розміру . Запишемо вихідне рівняння (1.13) у виді 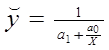. Тоді, якщо покласти

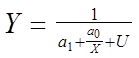 ,                                   (1.14)

те перетворене рівняння

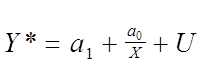 ,                      (1.15)

буде лінійним щодо параметрів і обурення.

Четверте припущення полягає в тому, що вихідна специфікація взаємозв'язку між перемінними (1.5) або перетворена (1.7) повинна супроводжуватися поруч гипо-тез про властивості розподіли імовірностей для випадкового воз-мущения. Ці гіпотези відносяться до його математичному ожи-данию, дисперсії і ковариациям. Найпростіший із можливих варіантів - прийняти математичне чекання рівним нулю, дисперсію - постійної і  зависящей не від Х, а різні значення U -  зависящими не друг від друга. Якщо і - номер спостереження, тобто  номер рівня ряду в табл. 1.1, і U_і –    випадкове обурення , що соот-ветствует цьому рівню, то упомя-нутые гіпотези можна записати у виді:

 ,                              (1.16)

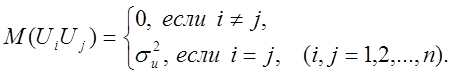 (1.17)

Тут  - невідома, але постійний розмір.

1.2 Однофакторные функції купівельного попиту. Коефіцієнти еластичності

У практику планування і прогнозування попиту на окремі товари і послуги часто використовуються аналітичні моделі попиту і споживання, що будуються у виді урав-нений, що характеризують залежність споживання товарів і послуг від тих або інших чинників. Такі моделі можуть бути одно-факторными і багатофакторними. Розглянемо однофакторные моделі залежності попиту від прибутку або ціни.

Основним чинником при аналізі купівельного попиту є прибуток населення. Однофакторные функції попиту Y на окремий товар від прибуткуZвивчалися німецьким економістом Энгелем, і відповідним цим функціям криві = f (Z) називаються кривыми Энгеля. Форми цих кривих для різних товарів можуть бути різні. Якщо попит на даний товар зростає приблизно пропорційно прибутку, то функція буде лінійної (мал. 1.5а). Такий характер має, наприклад, попит на одяг, фрукти. Якщо ріст значень попиту, починаючи з визначеного моменту, у міру насичення попиту, відстає від росту прибутку, то крива Энгеля має вид увігнутої кривої (мал.1.5б). Наприклад, такий характер попиту на товари першої необхідності. Нарешті, якщо в міру зростання доходів попит на дану групу товарів зростає усі більш високими темпами, то крива Энгеля опукла (мал. 1.5в). Так змінюється попит на предмети розкоші.

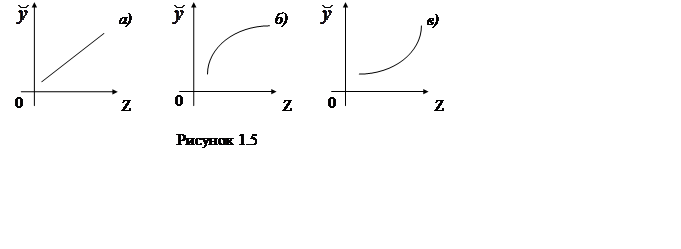Той же принцип розмежування груп товарів по типах функцій попиту від прибутку використовував шведський економіст  Л.Торнквист, що запропонував спеціальні види функцій попиту (функції Торнквиста) для трьох груп товарів: першої необхідності, другої необхідності і предметів розкоші.

Функція Торнквиста для товарів першої необхідності має вид

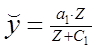                                     (1.18)

і відбиває той факт, що ріст попиту на ці першочергові то-вары з ростом прибутку поступово сповільнюється і має межа а_1. Графік функції є увігнутої кривої. Функція попиту по Торнквисту на товари другої необхідності виражається фор-мулой

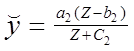 ,   Z b₂.                                             (1.19)

Ця функція також має межу а₂, але більш високого рівня, при цьому попит на цю групу товарів з'являється лише після того, як прибуток досягне розміру b₂; графік функції – во-гнутая крива. Нарешті, функція Торнквиста для предметів розкоші має вид

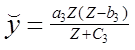 ,   Z ≥ b₃.                          (1.20)