Економетрика: Навчальний посібник (Уведення. Розділ "Моделі з двома перемінними"), страница 7

характеризує відхилення перемінної Y від розміру ў, вычи-сленной по функції регресії (1.2), і називається возму-щением (возмущающей перемінної). Вона включає вплив неврахованих чинників - переменных, випадкових перешкод і помилок спостережень. Її значення змінюється для кожного спостереження. З (1.2) і (1.3) випливає, що залежну перемінну Yможна представити у виді

Y = f (X, a_0, a_{1, …}, а_m) + U,                          (1.4)

де а_0, a_{1,  ...,} a_m - невизначені коефіцієнти. Такий вид запису дозволяє також інтепретувати випадкову перемінну U як враховуючу неправильну специфікацію функції регресії, тобто  неправильний вибір форми рівняння, що описує шукану залежність. Завдяки уведенню випадкової перемінної U, перемінна Yтакож стає випадкової, оскільки при заданих значеннях Х їй не можна поставити у відповідність тільки одне визначене значення. У той час як дослідник має у своєму розпорядженні значення объяс-няет і объясняющей перемінних    спостережень , що у результаті спільних , над ними,значення возмущающей перемінної U безпосередньо одержати не можна, оскільки вона являє собою конгломерат багатьох що важко враховуються і випадкових впливів. Лише після кількісної оцінки функції регресії можна знайти значення возмущающей перемінної U.

Третє припущення полягає в можливості оценивания параметрів а_0,  а₁,…,а_m функції регресії (1.2). Класичний регресійний аналіз оцінок …, параметрів a₀, a₁, _..., а_m рівняння регресії (1.4) заснований на методі найменших квадратів (див. § 1.5), що устанав-ливает деякі обмеження на вид функції регресії:

а) параметри а₀, а₁,…,а_m повинні входити у вираження для функції регресії в рівнянні (1.4) линейно, тобто

Y = а₀ + а₁ f₁(X) + ... + a_m f_m (X) + U ;                  (1.5)

  б) якщо в якості вихідній моделі обрана нелінійна щодо параметрів модель, то передбачається, що й обурення U входить у неї нелінійно:

Y = f (X, a₀, a₁,…,a_m,U)...                     (1.6)

Крім того, повинне існувати деяке перетворення над рівнянням (1.6) таке, що

g (Y) = g (f (X, a₀, a₁,…,a_m,U))=+g₁(X)+.....+ g_m (X) + U.

Тоді рівняння

 =  + g₁(X) + ... + g_m (X) + U        (1.7)

буде лінійним (щодо параметрів і обурення) урав-нением моделі. Нелінійне рівняння (1.6) ідентично исход-ной моделі; лінійне регресійне рівняння (1.7) є найважливішою складовою частиною перетвореної оцінюваної моделі. Часто виконуваними перетвореннями є, наприклад, логарифмування і знаходження зворотного значення.

Приклад 1 Нехай необхідно охарактеризувати зависи-мость врожайності Y деякої сільськогосподарської культу-ры від кількості Х внесених добрив. У даному випадку в якості однофакторной виробничої функції можна вибрати функцію виду

 =a₀ + a₁ X - a₂ X²   (a₀>0,   a₁>0,   a₂>0).            (1.8)

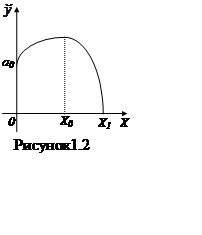При відсутності добрив уро-жайность складає а₀ одиниць. З увели-чением кількості внесених удобре-ний відбувається спочатку зростання врожайності, і в крапці  Х = Х₀ вона дос-тигает найбільшого значення. Дальней-шее нарощування витрат добрив виявляється нерозумним. Воно приводить до зниження врожайності і навіть повній її втраті при Х = Х₁ (мал. 1.2).

Функція регресії (1.8) залежить від невідомих коэф-фициентов а_0, а₁, а₂  линейно і, отже, відповідно до (1.5) зв'язок випадкових перемінних Y і X необхідно задати у виді

Y = a₀ + a₁X - a₂X²  + U,                             (1.9)

де U - випадкове обурення.

Приклад 2 При моделюванні ситуацій, у яких ріст витрат Х деякого ресурсу R веде до необмеженому увели-чению випуску Y, може бути використана статечн виробнич функці

    (а₀  > 0,   а₁ > 0).                      (1.10)

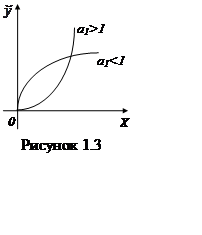Наскільки швидко зростає випуск Yзави-сит, мабуть, від розміру параметрів а₀ і а₁. При а₁ > 1 статечна функція (1.10) є опуклої, при a₁ < 1 - увігнутої (мал. 1.3).

Вихідна модель (1.10) – нелиней-на щодо параметрів а₀ і а₁. У цьому випадку відповідно до (1.6) і (1.7) необ-ходимо покласти