Економетрика: Навчальний посібник (Уведення. Розділ "Моделі з двома перемінними"), страница 6

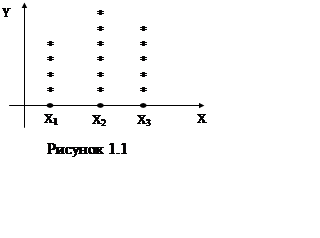
Стохастическая залежність між Y іХ зв'язана з тим, що зависи-мая перемінна, крім виділеної перемінної Х, підпадає під вплив так-же ряду неконтрольованих або неврахованих чинників, а також тим, що наклады-ваются помилки виміру. Оскільки значення залежної перемінної схильні случай-ному розкиду, вони не можуть бути предсказаны з достатньою точністю, а тільки з визначеною імовірністю.  Значення , що появляю-тся , залежної перемінної Y є реализа-циями випадкового розміру. Випадкової називається розмір, що приймає в результаті випробування то або інше (але при цьому тільки одне) можливе значення, заздалегідь невідоме і мінливе від випробування до випробування.

Стохастическая залежність (1.1) є односторонньою і називається регресією. Регресія встановлює залежність однієї випадкової перемінної від інший (парна регресія) або декількох випадкових перемінних (множинна регресія). Одностороння стохастическая залежність виражається з помо-щью функції, що, для відмінності її від суворої математи-ческой функції, називається функцією регресії або просто регресією. Існує принципова різниця між функ-циональной залежністю і регресією. При функціональній залежності аргумент Х цілком визначає значення функ-ции Y. Крім того, при функціональній залежності функція може бути  оборотна  (функція Х= є  зворотної до  функції Y = Х³). Функція регресії цією властивістю не володіє. З огляду на це, розрізняють регресію Y на Х(якщо досліджують стохастическую залежність Y від Х) і регресію Х на Y (якщо вивчають стохастическую залежність Х від Y). Наприклад, при вивченні механізму зв'язку між ціною товару (Х) і попитом (Y) практичний інтерес представляють обидві постановки завдання: залежність ціни товару від попиту, а також зворотна залежність - попиту від ціни товару, тому що измене-ние цін на товари відбивається на попиті населення. У цьому випадку окремо будуються регресіїY на Х и Х на Y. Обидва перемінні є тут випадковими. Кожному значенню Х відповідає безліч значень Y і, навпаки, кожному значенню Y відповідає безліч значень Х. Якщо ж логічне тлумачення залежності між двома перемінними можливо тільки в однім напрямку, як, наприклад, при дослідженні впливи кількості внесених добрив або  осадів , що випасли , (Х) на врожайність сільськогосподарських культур (Y), то знаходиться тільки одна функціярегресії Y на Х. Стохастическая залежність Х від Y у даному випадку не мають змісту.

Друге припущення перебуває в здійсненні специ-фикации форми зв'язку між Y іХ. Содержательные сообра-жения, на основі яких було прийняте співвідношення (1.1), повинні прояснити і його конкретну функціональну форму або підказати додаткові умови, якою повинні задовольняти параметри моделі. Оскільки тим самим   умовам можуть задовольняти різні функції, прийдеться звернутися до статистичного аналізу і з його допомогою осу-ществить вибір серед можливих альтернативних варіантів. У випадку парной регресії (стохастической залежності резуль-тативной перемінної Y від однієї объясняющей перемінної Х) завдання полягає у установленні виду функції регресії

 = f (X, a_0, а_1,..., а_m ),                             (1.2)

де а₀, а₁, ..., а_m - невідомі параметри.

Знаходження функції регресії відбувається по эмпири-ческим даним (табл. 1.1), що містить випадковості і вплив другорядних причин, що своєю мінливістю зату-шевывают і спотворюють щирий зв'язок. У силу того, що случай-ности і другорядні чинники не можуть бути виключені з досвідчених даних, залежність міжY і Xнабуває стохастический характер.

Т а б л и ц а  1.1

Випадковий розмір

 U = Y - ў                                       (1.3)