Економетрика: Навчальний посібник (Оцінювання результатів спостережень над нормально розподіленою випадковою величиною. Проверка статистических гипотез)

Таким образом, 100(1-)% доверительный интервал для неизвестного параметра qприобретает вид              (2.64)

Здесь величина

называется точностью оценки. Часто пишут ±

Пусть, например, необходимо найти истинное значение некоторой величины q. С этой целью проведено n³50 измерений этой величины и вычислены среднее выборки  и выборочная дисперсия s². При n50 с большой степенью точ-ности можно считать, что . Предположим, что резуль-таты выборки подчиняются нормальному закону . Тог-да, согласно (2.23), ~, и доверительная оценка математического ожидания q при известной дисперсии будет следующей :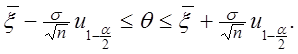             (2.65)

Если точность 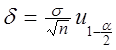 доверительной оценки (2.65) задана, то необходимый для ее обеспечения минимальный объем выборки должен быть, очевидно, равным .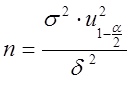

Например, при    из приложения Б находим 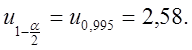 Следовательно, 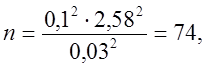т. е. при стандарте  и доверительной 99% вероятности точность результата измерения , равная  (±0,03), достигается при минимальном числе наблюдений    n = 74.

Задача 2 Оценка параметра q при неизвестной дисперсии . На практике обычно число наблюдений n невелико и дисперсия  наблюдаемой величины  неизвестна, тем более неизвестна дисперсия  оценки . В этом случае  используем  t-статистику Стьюдента (2.45)

.

Как уже отмечалось, она не зависит от генеральной дисперсии . Используя (2.63), находим

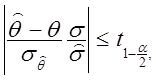
где t_{p ­}- квантиль распределения Стьюдента. Доверительный )% интервал для параметра q таков : 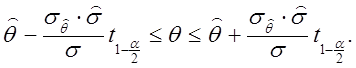            (2.66)

Для оценки  дисперсия  а оценкой генеральной дисперсии является выборочная дисперсия s²  , имеющая r =n - 1 степеней свободы. Доверительная оценка (2.66) приобретает вид 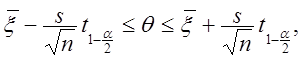                (2.67)

где квантиль  соответствует распределению Стьюдента с n-1 степенями свободы.

Пусть, например, в результате выборки объема n= 9 получены значения  и  Тогда при уровне значимости  и r=n–1=8 из приложения В находим  

       Следовательно, имеем  т.е. с доверительной 95% вероятностью

Задача 3 Оценка дисперсии . Роль дисперсии неоднократно подчеркивалась в предыдущем изложении. Не говоря о том, что знание генеральной дисперсии  позволяет получать удобные оценки параметра q, например, (2.65), дисперсия имеет и самостоятельную ценность как информация о точности применяемой методики. Воспользуемся тем фактом, что величина (2.38) 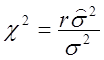 является ²-статистикой, т. е. удовлетворяет ²-распределе-нию с r степенями свободы (дисперсия имеет r степеней сво-боды). Поскольку распределение Пирсона несимметрично, то здесь необходимо воспользоваться равенством (2.62), откуда получаем 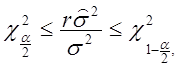,т. е. доверительный 100(1-)% интервал для имеет вид 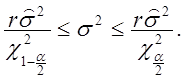                           (2.68) В частности, если  - выборочной дисперсии с n - 1 степе-нями свободы,

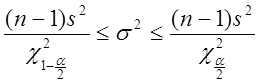.                   (2.69)

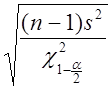
Отметим, что из (2.69) можно получить 100(1-)% доверительный интервал для стандарта :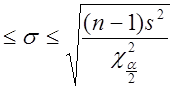.                (2.70)

Пусть результаты 9 наблюдений являются реализациями нормально распределенной по закону N величины. Вычислена выборочная дисперсия и она равна s² = 0,5. При 90% доверительной вероятности и числе степеней свободы r=8 из приложения Г находим   Тогда   или  Соответствующий интервал для :

Задача 4 Оценка разности математических ожиданий двух нормальных величин с общей дисперсией. Предположим, что выборка объема n₁ из  распределения и выборка объема n₂ из  распределения. Считаем, что оценки  и параметров а₁ и а₂ линейно зависят от результатов наблюдений. Тогда

 ~  ~

Рассмотрим случайную величину  Очевидно, она распределена нормально по закону

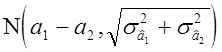 ~.Здесь дисперсии  и имеют r₁ и r₂ степеней свободы соответственно. Дисперсию  можно оценивать средневзвешенной дисперсией

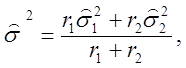                   (2.71)

число степеней свободы у которой равно r₁ + r₂. Здесь оценка дисперсии  для первой выборки; для второй. По аналогии с (2.45) t-статистика Стьюдента в данном случае приобретает вид 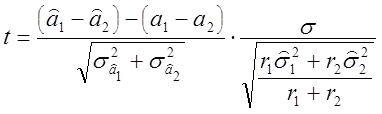.            (2.72)

Она имеет r₁+r₂ степеней свободы. Доверительный интервал для разности а₁ - а₂  может быть получен из (2.63), как и в задаче 2.

Рассмотрим частный случай, когда   Тогда 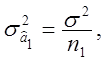 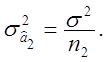 Выберем в качестве оценок генеральной дисперсии выборочные дисперсии :   Средне-взвешенная оценка дисперсии , таким образом , будет равна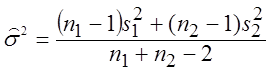                          (2.73)с числом степеней свободы n₁+n₂-2. Для статистики (2.72) получаем выражение

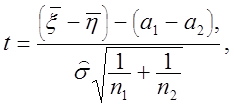                       (2.74)

где  определено в (2.73). Как и следовало ожидать, оно не зависит от генеральной дисперсии . В результате приходим к следующему   100(1-)% доверительному интервалу для разности а₁ - а₂ :

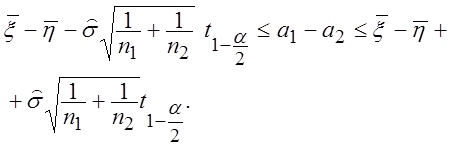            (2.75)

Задача 5 Оценка отношения двух дисперсий. Пусть наблюдения  и  двух случайных величин  и  распределены нормально по законам  и соответственно. Если  и  - оценки  и имеющие r₁ и r₂ степеней свободы, то, согласно (2.51), величина