Економетрика: Навчальний посібник (Оцінювання результатів спостережень над нормально розподіленою випадковою величиною. Проверка статистических гипотез), страница 2

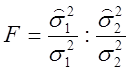
имеет F-распределение с r₁ и r₂ степенями свободы. Поскольку распределение Фишера асимметрично, то из (2.62) получаем 100(1-)% оценку

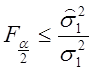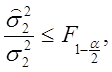:                              (2.76)

где -квантили F-распределения. После несложных преобра-зований с учетом (2.55) приходим к следующему 100(1-)% доверительному интервалу для отношения двух генеральных дисперсий

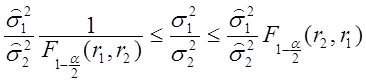.             (2.77)

В иллюстративных целях рассмотрим следующий пример. Пусть n₁ = 10, n₂ = 20. В качестве оценок  и  дисперсий и  выбраны выборочные дисперсии  и , и по результатам выборок получены значения   90% довери-тельный интервал имеет вид

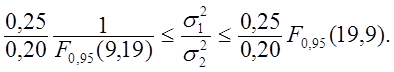
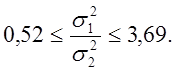По таблицам приложения Д находим :   Таким образом,  Отметим, что полученный доверительный интервал содержит 1, и, следо-вательно, данные согласуются с гипотезой равных дисперсий (см.§2.6).

Если в (2.76) положить , т. е.  и  - оцен-ки одной и той же генеральной дисперсии , то в этом случае

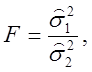
и, следовательно, F-распределение может быть использовано для оценки отношения двух оценок одной и той же дисперсии. Со 100(1-% вероятностью из (2.77) получаем

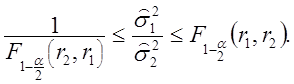                      (2.78)

2.5 Проверка статистических гипотез

При построении интервальных  оценок генеральных параметров (см.§ 2.4) использовался принцип практической достоверности: события с вероятностью, близкой к 1, считаются практически достоверными. Это позволило не доводить окончательные вероятности до 1 (что дало бы бесконечные интервалы в качестве границ). Принимаемый при этом уровень достоверности назывался доверительной вероятностью р.

Из принципа практической достоверности вытекает принцип практической невозможности: события с малыми вероятностями, близкими к 0, считаются практически невоз-можными. В качестве примера использования этого принципа может служить правило 3 в случае нормального распре-деления (см.§ 2.3).

Случайное событие в результате наблюдения может происходить, а может и не происходить. Практически невозможное событие, таким образом, можно считать неслучайным. Говорят, что оно является значимым. Использование принципа практической невозможности для доказательства неслучайного появления события с малой вероятностью называется принципом значимости. Наибольшее значение вероятности, при котором событие считается неслучайным (значимым), называется уровнем значимости. Чем выше уровень значимости, тем он “жестче”, ибо тем большее число событий нельзя рассматривать как случайные. Очевидно, уровень значимости  и уровень достоверности р как вероятности противоположных событий в сумме должны давать единицу :

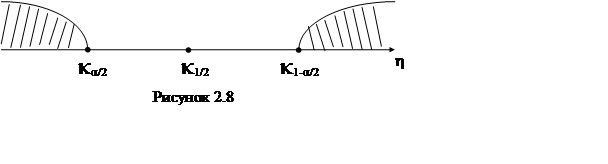
Значимые события были построены нами в предыдущем параграфе. Действительно, если  - случайная  величина с известным законом распределения, то при заданном уровне значимости a можно найти симметричные относительно медианы распределения квантильные доверительные границы  и  (2.62). Значения , меньшие чем и большие, чем  образуют область G (рис.2.8). При значениях  близких

к нулю, событие  Î G становится практически невозможным и, следовательно, значимым. Область G образует область значимости для случайной величины

Принцип значимости лежит в основе проверок так назы-ваемых статистических гипотез. Под статистической гипотезой понимают всякое высказывание о виде неизвестного распределения или о параметрах известного распределения. Рассмотрим вторые.

Пусть относительно некоторого генерального параметра q выдвигается гипотеза H₀  : q  = q₀,

где q₀ - некоторое число. Такую гипотезу будем называть нулевой. Гипотеза H₁ : q  ¹ q₀

называется альтернативной (конкурирующей).

Гипотеза H₀ может быть принята или отклонена на основании результатов наблюдений. Если нулевая гипотеза и данные выборки согласованы, то мы будем считать, что она подтверждается данными; в противном же случае гипотеза H₀ не согласована с данными, и мы будем говорить, что они значимо отклоняются от гипотезы.

Принимая решение относительно истинности или ложности гипотезы, мы можем допустить ошибку. Возможные ошибки различаются по своему характеру. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. При заданном уровне значимости a

Р (отклонить Н₀, когда верна Н₀)=a,

т. е. вероятность ошибки первого рода достаточно мала. Ошибка второго рода состоит в том, что гипотеза принимается , а на самом деле она неверна

P (принять Н₀, когда верна Н₁)=b.

Правильное решение также может быть двух родов:

P (принять Н₀, когда верна Н₀)=1-a;

P (принять Н₁, когда верна Н₁)=1-b.

Вероятность 1-b=P(H₁/H₁) называют мощностью критерия.