Економетрика: Навчальний посібник (Оцінювання результатів спостережень над нормально розподіленою випадковою величиною. Проверка статистических гипотез), страница 3

 Одну и ту же статистическую гипотезу можно проверить с помощью различных случайных величин. Каждый такой способ проверки называется критерием значимости. Из всех воз-можных критериев обычно стараются выбрать тот, у которого при заданном уровне значимости меньше вероятность ошибки второго рода. Наиболее употребительными на практике являются критерии Стьюдента, Пирсона и Фишера, которые  используют t-статистику (2.45), c²-статистику (2.37) и F-статистику (2.51) соответственно в качестве случайной величины.

Если выбрана соответствующая случайная величина (статистика) , то при заданном уровне значимости a для параметра q может быть построена интервальная оценка  с доверительной вероятностью р = 1-a. Вообще говоря, истинное значение q может равняться любому числу из доверительного интервала. Таким образом, если , у нас нет оснований отвергать нулевую гипотезу. С другой стороны, если q₀ не попадает в доверительный интервал, то соответствующее значение  статистики  окажется в области значимости G, и, согласно принципу значимости, оно становится практически невозможным. Следовательно, мы должны принять гипотезу  и, тем самым, отвергнуть гипотезу Н₀.

При проверке статистической гипотезы область значимости G называют критической областью гипотезы. Квантильные доверительные границы  и  (рис. 2.8) называются критическими значениями гипотезы. Гипотеза Н₁ в данном случае является двустороннейи ее можно разложить на две гипотезы:

:q  < q₀ и :q  > q₀.

Если одно из указанных здесь неравенств заведомо невозможно, то альтернативную гипотезу Н₁ называют односторонней и для ее проверки применяются односторонние критерии значимости (в отличие от обычных двусторонних).

Односторонний критерий можно получать из двусто-роннего. Обратимся к рис. 2.8. Пусть, например,  есть t-стати-стика Стьюдента (2.45). Если q  > q₀ , то, очевидно, и оценка  (значения , меньшие q₀, не представляют интереса или считаются практически невозможными). Тогда 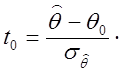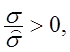т. е. значение t₀ попадает в правую часть критической области 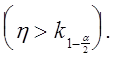В случае q <q₀ имеем  и  Значит, t₀ будет принадлежать левой части критической области 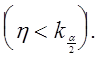 Если мы заранее знаем, что возможно лишь одно из неравенств, то рассматривать мы должны лишь одну из половин критической области. Вероятность попадания в критическую область уменьшается, тем самым, ровно вдвое и станет равна  

Желая сохранить вероятность ошибки первого рода (она равна a) неизменной, выбираем для одностороннего критерия тот же уровень значимости, что и для двустороннего, т. е. a. Тогда для односторонней гипотезы Н₊ критическая область гипотезы будет иметь вид  для  . Так как и  то критическая область односторонней гипотезы будет шире соответствующей критической области двусторонней гипотезы. Следовательно, при одностороннем критерии большее число значений  придется считать неслучайными (значимыми), большее число нулевых гипотез будет отвергнуто. Это означает, что односторонний критерий значимости имеет намного меньшую вероятность ошибки второго рода, чем соответствующий двусторонний. Отметим, что в случае распределения Стьюдента  (см. § 2.4).

Подведем итог. При уровне значимости a:

а) двусторонний критерий Стьюдента, отклоняющий нулевую гипотезу, имеет вид

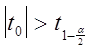;                                  (2.79)

б) односторонний критерий, имеющий меньшую ошибку второго рода, таков:

,    если q  > q₀;

,   если q  < q₀.                     (2.80)

Наиболее часто встречаются статистические гипотезы, связанные со сравнением различных выборок, когда приходится сравнивать различные методики анализа или различные условия производства.

Пусть  и - выборки из нормальных распределений  и ( Необходимо проверить нулевую гипотезу, что а₁ = а₂ или  Вычислим средние выборок и , а также выборочные дисперсии  и

Задача 1 Сравнение двух дисперсий. Необходимо проверить нулевую гипотезу  при конкурирующей  Воспользуемся критерием Фишера. Для этого рассмотрим доверительную оценку отношения двух выборочных дисперсий (2.78), которая в данном случае приобретает вид  .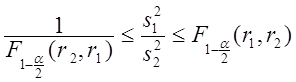

Согласно принципу значимости противоположные неравенства здесь невозможны, если справедлива нулевая гипотеза. Противоположные неравенства: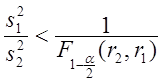,  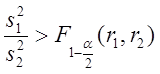(2.81) образуют критическую область двусторонней гипотезы, и если отношение  попадает в эту область, то различие между дисперсиями  и  следует признать значимым.

Пусть, например,  Если по смыслу задачи большей выборочной дисперсии заведомо не может соответствовать меньшая генеральная, т. е. неравенство  заведомо невозможно, то нужно применять односторонний критерий Фишера. Поскольку при небольших a обязательно