 рактеризує
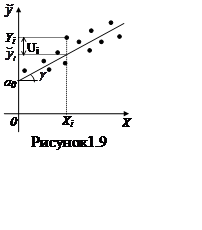
нахил прямої до осі ОХ. Якщо g
рактеризує
нахил прямої до осі ОХ. Якщо g![]() - кут,
який пряма регресії утворює з віссю абсцис, то а1 = tgg. Коефіцієнт а1 є мірою впливу змінної Х на змінну
- кут,
який пряма регресії утворює з віссю абсцис, то а1 = tgg. Коефіцієнт а1 є мірою впливу змінної Х на змінну
![]() Відповідно до рівняння (1.24) а1
показує величину зміни
Відповідно до рівняння (1.24) а1
показує величину зміни ![]() при зміні аргументу Х на
одну одиницю.
при зміні аргументу Х на
одну одиницю.
Якщо Х позначає об'єм виробництва деякої продукції,
а Y - сумарні витрати або витрати виробництва, то похідна виробничій
функції ![]() називається граничними витратами
виробництва. У випадку (1.24)
називається граничними витратами
виробництва. У випадку (1.24) ![]() тобто значення коефі-цієнта
а1 визначає величину граничних витрат виробництва.
тобто значення коефі-цієнта
а1 визначає величину граничних витрат виробництва.
Уявімо собі таку ситуацію. У виробництві продукції
використовується декілька видів сировини. Однак витрати всіх ресурсів строго
регламентовані технологією виробництва. Тільки один ресурс (наприклад, витрати
праці) може змінюватись, впливаючи на объем виробництва. Виробнича функція
(1.24) характеризує тут залежність випуску продукції Y від витрат Х
цього специфічного ресурсу. Швидкість зміни цієї функції виражається її
похідною ![]() і називається граничною продуктивністю
ресурсу. Якщо мова йде про витрати праці, то
і називається граничною продуктивністю
ресурсу. Якщо мова йде про витрати праці, то ![]() гранична
продуктивність праці. Отже, припускаючи, що виробнича функція має вигляд
(1.24), коефіцієнт регресії а1 у даному випадку визначає
граничну продуктивність ресурсу.
гранична
продуктивність праці. Отже, припускаючи, що виробнича функція має вигляд
(1.24), коефіцієнт регресії а1 у даному випадку визначає
граничну продуктивність ресурсу.
На практиці для оцінки впливу факторної ознаки X на результативну ознаку Y звичайно використовують коефіцієнт еластичності (1.21). У випадку лінійної регресії (1.24) коефіцієнт еластичності обчислюють за формулою
![]() , (1.25)
, (1.25)
де
![]() і
і ![]() -
середні ознак X і Y, знайдені за результатами вибірки. Параметр EX
показує, на скільки відсотків у середньому зміниться результативна ознака Y,
якщо факторна ознака X збільшиться на 1 % .
-
середні ознак X і Y, знайдені за результатами вибірки. Параметр EX
показує, на скільки відсотків у середньому зміниться результативна ознака Y,
якщо факторна ознака X збільшиться на 1 % .
У реальних економічних умовах зв'язок між змінними адекватно представляється, як правило, у нелінійній формі. Найпростіший спосіб у таких ситуаціях, на перший погляд, - апроксимація змінної Y за допомогою багаточлена від Х. Якщо припустити , що всі табличні значення Хі (і = 1, 2, ..., n) різні, то, як відомо з теорії інтерполяції, через n точок можна єдиним способом провести багаточлен ступеня n-1. Однак оскільки число спостережень n порівняно велике, ми будемо мати справу з багаточленами великого ступеня. Ясно, що нас цікавлять багаточлени, ступінь яких нижче можливого:
![]() m < n-1.
(1.26)
m < n-1.
(1.26)
При моделюванні немонотонних процесів багаточлени виду (1.26) набули широкого поширення. В статистиці, при вивченні часових рядів, вироблене правило вибору ступеня багаточлена (1.26), засноване на визначенні величин скінчених різниць рівнів заданих рядів. Відповідно до цього правила, багаточлен першого ступеня (пряма) застосовується як модель такого ряду, у якого перші різниці
![]() t = 1, 2 ,...,
n-1
t = 1, 2 ,...,
n-1
постійні. Якщо перші різниці не рівні, але варіюють із незначними відхиленнями одна від одної, а середня арифметична других різниць
![]() t = 1, 2,..., n-2
t = 1, 2,..., n-2
настільки мала, що нею можна знехтувати, то перші різниці вважають практично рівними. Аналогічно, якщо аналізуючи другі різниці, ми приходимо до висновку, що вони практично рівні, то для відображення ряду емпіричних даних використовують багаточлен другого ступеня (параболу) і т.д.
Як перше наближення при розрахунку вирівняних значень рівнів ряду динаміки, можна використовувати формулу
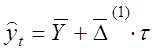 ,
, ![]() (1.27)
(1.27)
при рівних або майже рівних перших різницях і
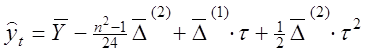 (1.28)
(1.28)
у
випадку рівних або майже рівних других різниць. Тут ![]() -
вирівняне значення ряду динаміки;
-
вирівняне значення ряду динаміки; ![]() - середній рівень ряду;
- середній рівень ряду;
![]() і
і ![]() - середні
арифметичні перших і других різниць відповідно;
- середні
арифметичні перших і других різниць відповідно; ![]() -
середній час.
-
середній час.
Розглянемо наступний приклад. Дано рівні виробництва
продукції на фірмі за перші 9 місяців 1997 року (див.табл. 1.4).
Розрахунки показують, що середня арифметична третіх різниць настільки мала, що
нею можна знехтувати і, як наслідок, другі різниці можна вважати практично
рівними. За формулою (1.28) одержуємо наступне рівняння тренда (тенденції), що
відображає розвиток досліджуваного процесу:![]()
![]()
У табл. 1.4 наведені вирівняні значення ![]() розраховані за рівнянням тренда.
розраховані за рівнянням тренда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.