Економетрика: Навчальний посібник (Однофакторные функції купівельного попиту. Коефіцієнти еластичності. Попередній аналіз даних. Побудова регресійних однофакторных функцій), страница 3

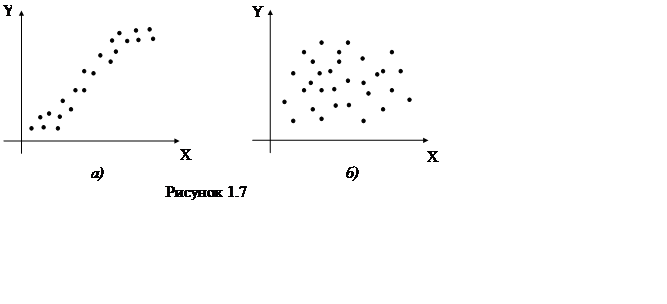
Cтійкість характеризує перевагу закономірності над випадковістю в зміні рівнів ряду. На графіках стійких рядів навіть візуально простежується закономірность (тенденція розвитку процесу), а на графіках нестійких рядів зміни послідовних рівнів ряду представляються хаотичними, і тому пошук закономірностей у формуванні значень рівнів таких рядів позбавлений змісту. На мал. 1.7 подані діаграми розсіювання, що відповідають стійкому (а) і нестійкому рядам (б). Висновок про стійкість  або нестійкість рівнів вихідних рядів даних можна зробити за шириною розкиду точок (X, Y) на площині. Якщо точки розташовані близько одна до одної у вигляді вузької смужки (мал. 1.7а), то можна стверджувати наявність стійкості і,

отже, між змінними Y і X спостерігається відносно тісний зв'язок. Якщо ж крапки розкидані широко по діаграмі (мал. 1.7б), то стійкості нема, і зв'язок між змінними Y і Х слабкий або, взагалі, відсутній.

Діаграма розсіювання дозволяє зробити візуальний аналіз емпіричних даних. Однак існують і більш точні, теоретично обгрунтовані методи виявлення закономірного зв'язку між випадковими змінними Y і X. Найбільш поширеним із них є метод Фостера - Стюарта. Він дозволяє не тільки установити наявність тенденції в зв'язку кількісних ознак Y і X, але і перевірити гіпотезу (1.17) про сталість дисперсії   показника . Суть методу полягає в наступному.

1   Порівнюється кожен рівень ряду з усіма попередніми, при цьому

        f_i  = 1,   e_i  = 0,   якщо Y_i  > Y_k ,   k=1, 2,..., i-1;

     f_i = 0,   e_i  = 1,   якщо Y_i < Y_k ,   k=1, 2,..., i-1;

     f_i = 0,   e_i = 0   в інших випадках.

2  Обчислюються значення величин

   .

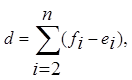
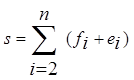Показники d і s характеризують тенденції у зв'язках Y і X та дисперсії  і Х відповідно.

3  За допомогою t-критерію Стьюдента  перевіряється гіпотеза про те,  чи можна вважати випадковими різниці d - 0 і . З цією метою знаходяться величини

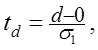
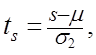                           (1.22)

де - середнє значення величини s;  і  - стандартні помилки величин d і s відповідно. Значення величин , і  табульовані і наведені в табл. 1.2.

4 При заданому рівні  порівнюються розрахункові значення t_d і  t_s  з табличними. Якщо t_d <  t_табл  і t_s < t_{табл ,} то гіпотеза про відсутність тенденцій у зв'язку Y і X та і Х  підтверджується.

Т а б л и ц я 1.2 - Значення середньої і стандартних помилок і  для n від 10 до 55

n
10	3,858	1,964	1,288
15	4,636	2,153	1,521
20	5,195	2,279	1,677
25	5,632	2,373	1,791
30	5,990	2,447	1,882
35	6,294	2,509	1,956
40	6,557	2,561	2,019
45	6,790	2,606	2,072
50	6,998	2,645	2,121
55	7,187	2,681	2,163

Як приклад  розглянемо визначення наявності тенденцій у ряду динаміки виробництва реалізованої продукції на виробничому об'єднанні за 1977 - 1996 р. (табл. 1.3). Дані наведені в порівняних цінах 1996 р.

Знаходимо d = 5, s = 7. За даними табл. 1.2 при n = 20 маємо:   . Підставляючи отримані значення у формулу (1.22), розраховуємо значення t_d і t_s, тобто

  

Найближче табличне значення t_табл для двостороннього критерію при n = 20 і рівні значимості   = 0,1  дорівнює  t_табл.=1,725  (див. додаток В), тобто  |t_d| > t_табл, |t_s| < t_табл. Отже, гіпотеза про відсутність тенденції в зв'язку і Х підтвердилася, а в зв'язку Y і X - відкинута, тобто  в ряду динаміки реалізованої продукції простежується деяка закономірність.

Т а б л и ц я 1.3 - Реалізована продукція виробничого об'єднання. Визначення f_i і e_i