Степенные ряды, страница 6

3)  

область сходимости

Доказательство. Выведем ряды для показательной и логарифмической функций.

1)  Посчитаем производные функции  и их значения в точке

Теперь эти значения подставляем общую формулу ряда Маклорена:

2)  Рассмотрим

А теперь заметим, что функция  является суммой ряда  Теперь воспользуемся теоремой о почленном интегрировании степенного ряда:

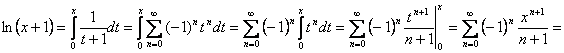
Ч.т.д.

Практическое применение рядов Маклорена связано с приближенными вычислениями. С помощью приведенных выше рядов можно посчитать примерное значение   и  а так же значения некоторых определенных интегралов, например,  Приближенное значение получается, когда вместо точного значения функции, которое сложно посчитать, рассматривается какая-либо частичная сумма соответствующего степенного ряда:

Но при таком отбрасывании бесконечного числа слагаемых неизбежно возникает погрешность.

            Определение. Погрешностью приближенного вычисления называется величина

Во многих случаях оценивать погрешность помогает следующая теорема.

            Теорема о погрешности. Если у знакочередующегося ряда все члены по абсолютной величине монотонно убывают, то погрешность не превышает модуля первого отброшенного члена:

            Пример. Вычислить с точностью до 0,01 значение

Представим   как  тогда можно воспользоваться разложением в ряд Маклорена функции  Область сходимости этого ряда  следовательно, его можно применять при

            Выпишем ряд:

    

Получившийся ряд – знакочередующийся,  и последнее слагаемое оказалось меньше погрешности

следовательно, по теореме о погрешности, если в качестве приближенного значения рассмотреть сумму первых четырех слагаемых, то требуемая точность будет достигнута.

            Пример. Вычислить  взяв первые три члена разложения подинтегральной функции в ряд Маклорена, оценить погрешность.