Теорема. Степенной ряд в интервале его сходимости можно дифференцировать почленно неограниченное число раз, причем получающиеся степенные ряды имеют тот же радиус сходимости, что и исходный ряд.
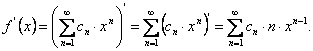
Теорема.
Степенной ряд можно неограниченное число раз почленно интегрировать в пределах
от 0 до ![]() если
если ![]() из
интервала сходимости ряда, причем получающиеся при этом степенные ряды имеют
тот же радиус сходимости, что и исходный ряд.
из
интервала сходимости ряда, причем получающиеся при этом степенные ряды имеют
тот же радиус сходимости, что и исходный ряд.
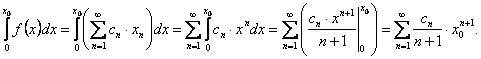
Пример.
Найти сумму ряда ![]()
Выше было
показано, что область сходимости этого ряда ![]() Преобразуем
ряд:
Преобразуем
ряд:
![]()
Ряд, котоый возник после
вынесения ![]() за знак суммы, является производной
от ряда
за знак суммы, является производной
от ряда ![]() т.е.
т.е. 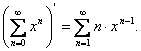
В предыдущем примере было
показано, что ![]() следовательно,
следовательно, 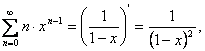 таким образом, для исходного ряда
получаем:
таким образом, для исходного ряда
получаем:
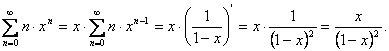
Теорема. Если
функция ![]() дифференцируема в точке
дифференцируема в точке ![]() неограниченное число раз, то она
может быть представлена в виде ряда Маклорена
неограниченное число раз, то она
может быть представлена в виде ряда Маклорена
![]()
Следует отметить, что
как всякий степенной ряд в точке ![]() ряд Маклорена
всегда сходится и, это видно из формулы, его сумма равна значению функции в
нуле. Но прежде чем применять разложение для других значений
ряд Маклорена
всегда сходится и, это видно из формулы, его сумма равна значению функции в
нуле. Но прежде чем применять разложение для других значений ![]() необходимо найти радиус сходимости
ряда и убедиться, что рассматриваемая точка принадлежит области сходимости.
необходимо найти радиус сходимости
ряда и убедиться, что рассматриваемая точка принадлежит области сходимости.
Доказательство. Предположим,
что нам удалось представить функцию ![]() в виде некоторого
степенного ряда:
в виде некоторого
степенного ряда:
![]()
Будем искать коэффициенты ![]() исходя из предположения, что и сам
ряд, и все его производные в нуле должны быть равны соответствующим значениям
исходной функции и ее производных. Прежде всего, подставим нуль в саму функцию:
исходя из предположения, что и сам
ряд, и все его производные в нуле должны быть равны соответствующим значениям
исходной функции и ее производных. Прежде всего, подставим нуль в саму функцию:
![]()
Мы получили значение нулевого коэффициента. Теперь будем считать производные и выводить формулы для последующих коэффициентов:
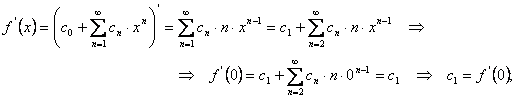


и т.д. Общая формула для коэффициентов ряда Маклорена будет иметь вид:
![]()
После подстановки полученных выражений в формулу ряда получаем:
![]()
Ч.т.д.
Ряды Маклорена для некоторых основных функций:
1) ![]() область
сходимости
область
сходимости ![]()
2) ![]() область
сходимости
область
сходимости ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.