Планирование и обработка результатов многофакторного эксперимента

Лабораторная работа №3 “Планирование и обработка результатовмногофакторного эксперимента”

Цель работы. По результатам активного эксперимента и  его обработки выявить взаимосвязи между факторами, определяющими ход химического процесса, и представить их в количественной форме – в виде математических моделей:

·  Модели первого порядка, учитывающей только линейные эффекты;

·  Неполной квадратичной модели, учитывающей линейные эффекты и эффекты взаимодействия факторов;

·  Полной квадратичной модели, дополнительно учитывающей квадратичные эффекты.   

Задача обработки результатов эксперимента заключается в определении наилучших оценок параметров той или иной модели и выбор ее в качестве основной для исследуемого процесса.

Предисловие

   Задачи и методы этой лабораторной работы аналогичны лабораторной работе № 2 и непосредственно связаны с построением математической модели с помощью метода  МНК. Если внимательно проанализировать точность оценок  полученных в результате обработки данных пассивного эксперимента в лабораторной работе №2, то можно заметить, что их значения существенно зависят от условий проведения эксперимента.

   Возможность обработки данных в реальном  масштабе времени привела, в частности, к развитию алгоритмических методов планирования эксперимента, основанных на последовательных процедурах обработки данных и планирования. Применение методов планирования эксперимента предполагает возможность проведения опытов в заданных  исследователем  условиях. Такой способ проведения эксперимента называют активным.

1.1  Основные понятия планирования эксперимента

 Определение 1.1

Множество всех точек проведения экспериментов

                                                          (1.1)

представляется с помощью матрицы плана

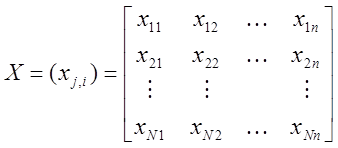             ,  где:    j–номер опыта;        i-номер фактора.     (1.2)

и называется планом эксперимента. (План  эксперимента, заданный с помощью матрицы   плана , будет в дальнейшем обозначаться через X.).

Определение 1.2                Точка

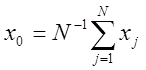                                                                                                                              (1.3)

называется центром плана (центральной точкой плана). Каждая координата  вектора  является средним значением  х координат всех точек плана

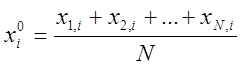                                                                                                         (1.4)

называется центральным, если его центр расположен в начале координат , т.е.                                                                                                                                                                                                       (1.5)

    Очевидно, что оптимальное планирование связано с разработкой планов, представляемых в некоторой стандартной форме. При этом целесообразно рассматривать центральные планы. Всякий план путем переноса начала координат может быть сделан центральным.

  Определение 1.3

    Область возможных значений независимых переменных называется областью    планирования эксперимента. Будем обозначать эту область Ω_x. Все точки  плана Х должны принадлежать области   Ω_x. Это требование мы будем записывать следующим образом:

                                                                                                                                       (1.6)

или

                                                                                                                                       (1.7)

Независимые переменные , как и в предыдущей работе, называют варьируемыми переменными или факторами. Область планирования эксперимента может быть задана, например, с помощью неравенств

                                                           .                                                       (1.8)

В этом случае говорят, что областью планирования является гиперкуб.

    В выражении (8) предельные (максимальное и минимальное) значения варьируемых переменных обозначены через +1 и -1 соответственно. Эти границы отвечают стандартизованному или нормированному масштабу изменения переменных. Переход к стандартизованному масштабу может быть осуществлен, например, следующим образом:

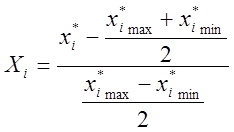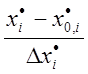                                             =.                                                    (1.9)

В формуле (1.9)  - значение переменной в натуральном масштабе измерения.

Определение 1.4

План Х называется ортогональным, если информационная матрица диагональная: