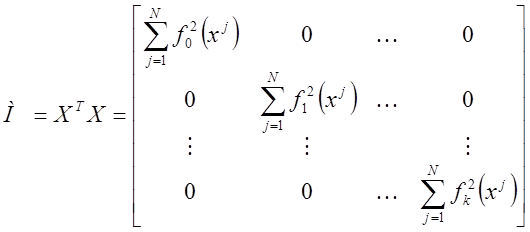Планирование и обработка результатов многофакторного эксперимента, страница 2

                         .                            (1.10)

  Матрица  размера (k+1)×(k+1) называется информационной матрицей Х. Здесь

  транспонированная матрица, а X -исходная матрица

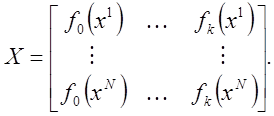
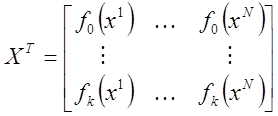                                                           (1.11)

Ясно, что информационная матрица плана Х зависит от выбора функций

Матрица  М  есть матрица системы нормальных уравнений из решения которой, как и в лабораторной работе №2, находятся оценки коэффициентов модели. Однако для ортогонального плана вычисления оказываются чрезвычайно простыми. Коэффициенты регрессии рассчитываются по следующим формулам:

        для  линейных эффектов 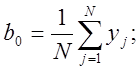 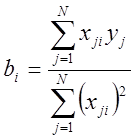                             ,              (1.12)

        для эффектов парного взаимодействия 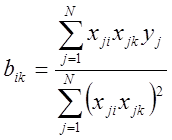               ,                      (1.13)

        для квадратичных эффектов 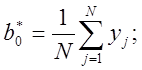 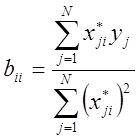                        .                      (1.14)

1.2   Построение математической модели,  описываемой полиномом первого порядка

  Вид модели

   Здесь будут рассмотрены планы, предназначенные для построения линейных моделей процессов вида

                                                                                                 (1.15)

Обозначив через X матрицу

                                                  

где  единичный вектор фиктивной - переменной 

                                                                                                                         (1.16)

получим для информационной матрицы плана выражение

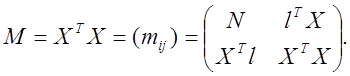                                                                                        (1.17)

Полные факторные планы

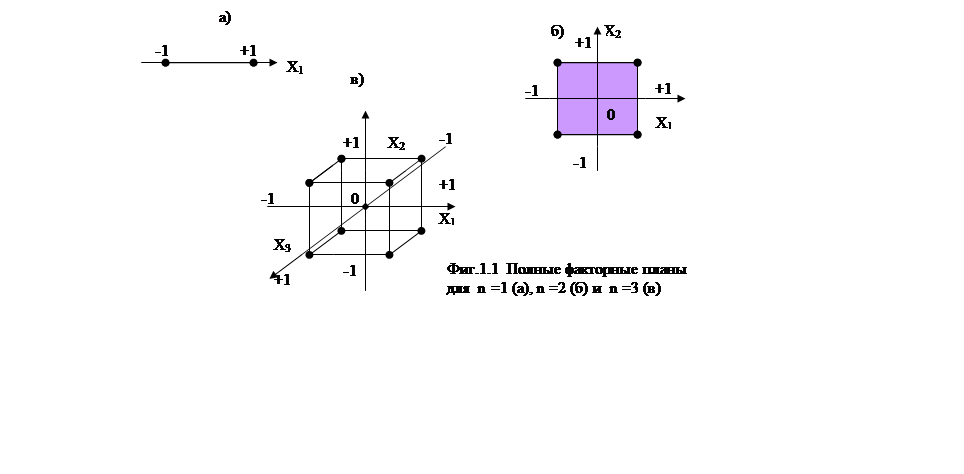
При отыскании линейной функции отклика (1.15) достаточно иметь два уровня каждого фактора, выбираемых симметрично относительно основного уровня: верхний и нижний. Для кодированных (стандартизованных ) факторов (1.9) эти значения суть +1 и -1.

Определение 1.5

Множество всех точек в n-.мерном пространстве, координаты которых являются +1(+) или -1(-), называется полным факторным планом типа 2ⁿ. Число точек  (опытов) в этом плане

                                                        N=2ⁿ.                                                                               (1.18)

При n, равном 1,2 и 3, матрицы планирования X для факторных планов 2ⁿ  имеют вид

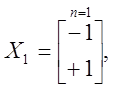
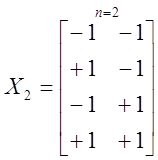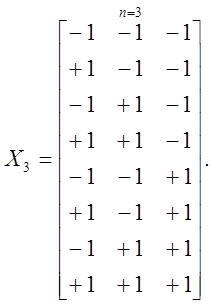           ,                                       (1.19)

Точки этих планов показаны на фиг.1.1. Легко получить следующее общее правило построения полных факторных планов.

Утверждение 1.1

Матрица планирования  факторного плана 2^{n +1} может быть получена с помощью матрицы Х_n плана 2ⁿ по формуле

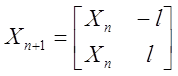                                             ,                                                                 (1.20)

где   определяется уравнением (1.16).

1.3.  Планы для моделей, содержащих линейные члены и взаимодействия различного порядка

Вид модели

При построении модели часто недостаточно принимать во внимание только линейные эффекты факторов, ибо влияние на целевую величину (в нашем примере выход целевого продукта) могут оказывать также взаимодействия факторов. В этом случае в модель необходимо вводить взаимодействия различных порядков. Модель принимает вид.

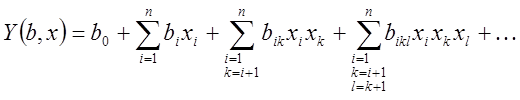                                                       (1.21)

Коэффициент  является мерой парного взаимодействия факторов (взаимодействия первого порядка), а коэффициент  отражает воздействие тройного взаимодействия (взаимодействия второго порядка). Для получения оценок коэффициентов модели типа (1.21) в принципе можно использовать полные факторные планы. Однако для числа факторов больше пяти целесообразно применять дробные факторные планы.